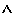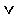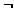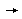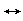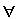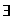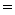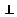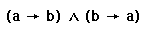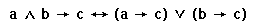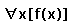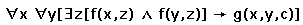The table below shows all the logic symbols used to enter formula's in Pandora.

Symbol Name	Logic Symbol	Input Character
And		^
Or		|
Not		~
Implies		>
If and only if		#
For All		A
There Exists		E
Equals		=
Top (true)		top
Bottom (false)		bottom

Valid names

All constants, predicates, functions and variables must have valid identifier names. A valid identifier begins with a lower-case letter, which is followed by any number of lower-case letters, numbers and underscore (_) symbols. For example, qwerty_345 is a valid name, but Qwerty is not (capitals are not permitted).

Using Quantifiers

When you use a quantifier (i.e. a for all or there exists symbol) in a logic formula you must use the following syntax, where Q is the quantifier v is a variable and F is the subformula you are using the quantifier on:

Qv[F]

The square brackets must be placed around the sub formula, but it is possible to use more then one quantifier on a subformula while only placing brackets around the actual subformula for example:

ExEyAz[f(x,y,z)]

Predicates and Functions

To use predicates and functions in Pandora enter the name of the function, or predicate followed by a list of all it's parameters separated by a comma's in set on round brackets. I.e. use the following syntax where P is the name and t1,...,tn are all terms:

P(t1,...,t2)

For example:

f(x,y,z)

If you want to specify a predicate of arity 0 then you can ommit the backets from your formula and just enter the name.

Pandora checks the signature of any formula you enter and may reject a formula if it contains a name which clashes with another name already defined in your proof

Examples

Here are some examples of formula's entered in pandora and their corresponding logic syntax

Input	Resulting formula
(a > b) ^ (b > a)
a ^ b > c # (a > c) | (b > c)
Ax[f(x)]
AxAy[ Ez[ f(x, z) ^ f(y, z) ] > g(x, y, c) ]