First-Order Logic (3)

< 1 2 3 >

Model theory is a way of attributing meaning to any given logic sentences. This is done by interpretation, the process of associating the sentence with some truth-valued statement about a chosen domain. This domain can be any set of our choice, for example the set of natural numbers. Here are some definitions associated with model theory:

• A model is an interpretation of a sentence that gives a true value (satisfies the sentence).
• An interpretation that does not satisfy a sentence is a counter-model for that sentence.
• A sentence with at least one model is satisfiable.
  • e.g. likes(sim, chocolate).
• A sentence with no models is unsatisfiable.
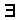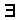  • e.g. xy(likes(x, y) 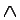¬likes(x, y)).
• A sentence in which every interpretation is a model, is valid.
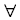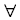  • e.g. xy(likes(x, y) 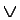¬likes(x, y)).
• A sentence (A) logically implies another sentence (B) if and only if every model for A is also a model for B, this is written as A |= B. This symbol is known as double turnstile.
  • e.g. 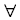x(likes(sim, x)) |= likes(sim, chocolate).
• Two sentences A and B are logically equivalent when each one logically implies the other, this is written as A 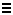B.
  • e.g. 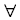x(¬likes(x, pain)) 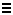¬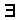x(likes(x, pain))