
|
Welcome to Duncan White's Fractal Koch Curve Page. I have written koch.cgi,
a Perl CGI script which draws Koch curves using a turtle graphics
implementation. Which you're welcome to use and play around with.
|
Create your own Koch Snowflakes
If you've ever read Benoit Mandelbrot's wonderful book "The Fractal Geometry of Nature", you'll have been as captivated by fractals as I am. There are many types of fractals - the gorgeously coloured Mandelbrot and Julia sets, artificial landscapes, artificial plants to name but a few. One of the simplest type of fractals are those called Koch curves, or Koch Snowflakes.Explaining these is a bit complex - maybe I'll fill this bit in later. Basically, a graphical turtle crawls around a regular polygon, turning and moving in a complex (but structured) way. The technique involves recursively replacing each straight line with a turtle trajectory, expressed as a sequence of move forward, turn left, turn right instructions.
Let's see the classic example: the Koch snowflake. Start with a triangle (the initiator). Replace each straight line with the following shape (the generator):
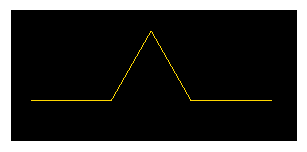
If you did this replacement recursively more and more times, you'd have a sequence of images as follows:

|

|

|

|
The above generator rule is described in terms of turtle movements as f+f--f+f where f means move forward, + means turn left 60 degrees and - means turn right 60 degrees.
Have you got the idea? Well, click here and have a play with the program.
Here's a few rules you might like to try:
- f+f--f+f - normal Koch snowflake (if on a triangle with 60 degree turns).
- f+f-f--f++f - interesting zigzag snowflake.
- f+f-f-f-f+f+f+f-f - the original Peano space-filling curve (use sides=4, angle=90).
- f-f++f-f - Cesaro's triangle sweep (use sides=4, angle=85).
You can download the Koch CGI script and it's support modules here.
D.White@ic.ac.uk Updated: September 2000
