 |
Generic Modelling of the Human Upper AirwayJoint project with Dr Peter Charters of University Hospital Aintree |
One major strand of my research is to create a generic model of the upper human airway. A generic model is one that replicates the geometry, kinematics and dynamics of the human airway and can be easily adjusted to replicate any specific instance of a human airway with reasonable accuracy. The model is constructed from data using modern techniques for shape, kinematic and dynamic modelling.
A generic model of the upper airway will have considerable value to anaesthetists, surgeons specialising in ear nose and throat and maxillary-facial areas, and medical instrument designers. Most fundamentally it will contribute to the understanding of the structure and function of the airway, and the factors that determine airway patency. It will provide new interactive ways of exploring and visualising the airway in different configurations such as head position during intubation and surgical procedures. It could be used to determine the accessibility of tumours destined for surgical removal, or to design implants to replace damaged or diseased bone. It could be incorporated in simulation training systems, replacing the current plastic models, which are inflexible and unrealistic. It could be used for the design of new airway instruments, providing vital information about accessibility and ergonomics. Since the model would be able to replicate the full diversity of the human airway, putative instruments could be tested thoroughly and optimised before expensive clinical trials are begun. This would cut the time and cost of evaluating a new instrument considerably, and lead to better design. Finally, such a model could be used for pre-operative assessment of patients, warning of difficulties that could be encountered during anaesthesia or surgery and indicating the best choice of airway instruments to use. Difficult airway management remains one of the most problematic areas in anaesthesia. Serious problems occur in certain patients including the damage of the upper incisor teeth, lesions of upper airway tract, oesophageal trauma, hoarseness and laryngeal injury and even cardiac arrest with brain damage. In the most serious cases, failed intubation may be the cause of death of a patient. Accurate pre-operative prediction of difficult cases is therefore a highly important area of research.
The creation of a generic model of the airway is a difficult task, and many research issues remain unaddressed. The problems result from the complexity of the airway, both in its geometric shape, its physical properties and its moving parts. The geometry shows considerable variation from subject to subject, not merely in size but also in subtle variations of shape. The rigid parts defined by the bones of the mandible and maxilla can be readily identified in CT images, and can be encoded into shape models. However, softer parts such as the soft palate and epiglottis are harder to identify in the images and to characterise. Little information has been published about the physical properties of the deformable parts of the airway, in particular the tongue. What is known is that its deformation is highly non-linear. Initially it behaves in an elastic manner as the blood is squeezed from it, then it becomes almost incompressible. To make things more complex the tongue displays a phenomenon known as stress relaxation. That is after deformation, for example with a laryngoscopic blade, it can be maintained in the deformed position with a force that decreases with time. All these natural properties make it very difficult to apply engineering methods, such as the finite element modelling method to model the deformation. Lastly, the airway contains a number of mobile parts, which are constrained in complex ways. The mandible is the simplest and is hinged in a well-understood manner. There is however a complex system comprising the floating hyoid bone and the epiglottis. The anaesthetists know its behaviour in practice, since the epiglottis may be raised, revealing the vocal chords by pushing the hyoid bone with the tip of a laryngoscope blade. The nature of this kinematic system is, however, not sufficiently understood to encode it in a computer model. Another moving part is the larynx, which, apart from being highly mobile during swallowing, is also elevated forward with the epiglottis during laryngoscopy. Although the difficulties are considerable, progress on some of the modelling issues over the last ten years has been encouraging, and has been greatly aided by the considerable increase in computer power and memory size. Much previous work on the airway has been directed towards the problem of predicting patients that will prove difficult to intubate during laryngoscopy by the anaesthetist.
The "Osseous Factors" Airway Model |
||
|
||
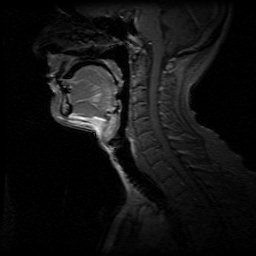
| Preliminary x-ray laryngoscopy studies were the basis for an early model the upper airway that had the objective of determining the causes of difficult intubation. The Osseous Factors Model of Peter Charters is shown on the left. Four points are used to determine geometry of the mouth and the space available for compression and displacement of the tongue. A computer simulation of this model was implemented and investigated. A screen shot of this is shown on the right. |
The osseous factors model was purely concerned with geometric features of the upper airway. Work to model the effect of the deformation of the tongue was investigated using the technique of finite elements. Initial modelling used only two-dimensional information ( Rodrigues Gillies and Charters 1998 ). Two-dimensional modelling simplifies the acquisition of the data, requiring only a mid-saggital image to estimate the tongue size. Incorporating laryngoscope blade shape into the model was possible and this work was the first credible explanation as to why a curved blade could produce a view as good as or better than a straight blade (Marks 1991). However the 2D model was soon found to be inadequate. The usual technique of rigid blade laryngoscopy involves displacement of the tongue to the left, and can only be represented in a full three-dimensional model. Subsequent studies using 3D finite element modelling, demonstrated that it is possible to simulate, with a reasonable degree of accuracy, the behaviour of the tongue as it is displaced by a laryngoscope blade, and hence predict whether the vocal cords can be seen ( Rodrigues Gillies and Charters 2001 ).
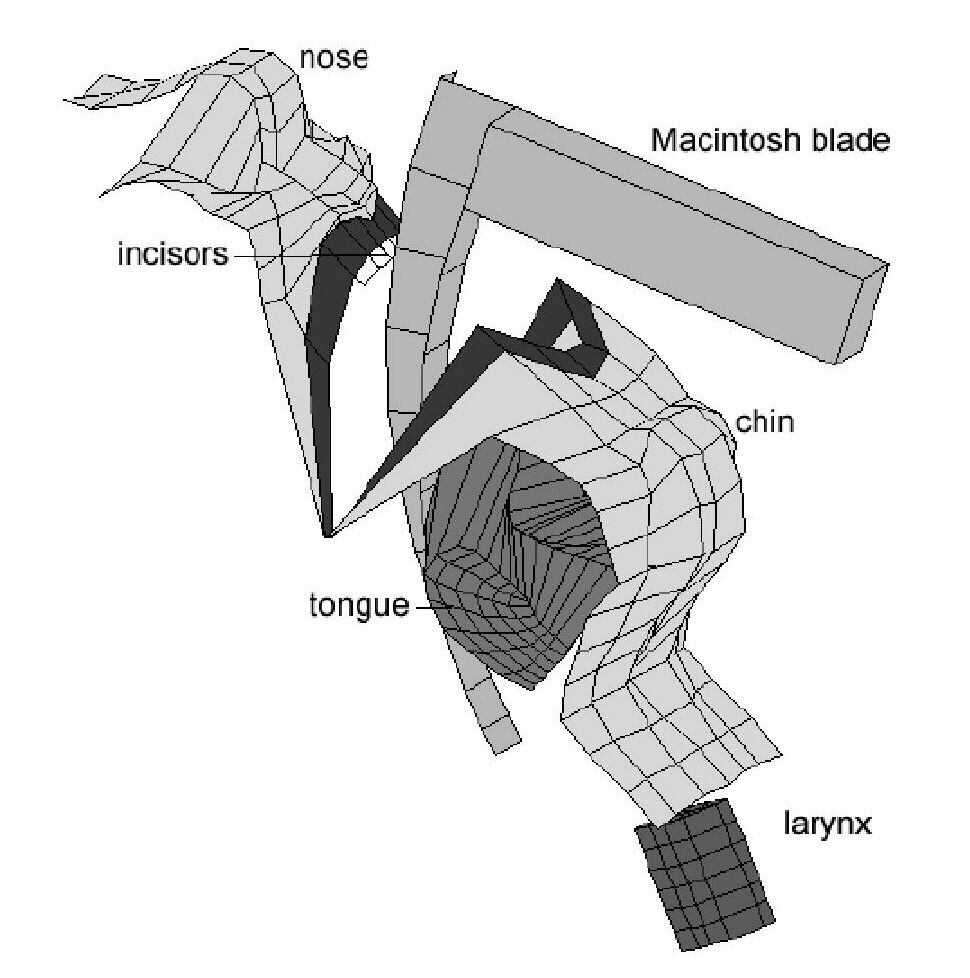 |
Three dimensional finite element simulation of the tongue during LaryngoscopyDuring the simulation the tongue is compressed and displaced to the side of the mouth uing a rigid blade laryngoscope. Validation was carried out using preoperative MRI scans and photographic records taken during laryngoscopy. From (Rodrigues Gillies and Charters 2001) |
A major difficulty in using the physical model of the tongue is data acquisition. It is necessary to begin with a magnetic resonance scan of the upper airway, from which the geometry of the tongue and mandible are segmented, then converted into a form where finite element modelling can be performed. This is a time consuming task requiring considerable specialist knowledge and expertise. Ideally, anaesthetists would like to be able to take a relatively small number of “bedside” measurements from a patient, enter these into a computer system and receive an assessment of intubation difficulty rapidly. Despite an enormous amount of work by many other groups in recent years this has continued to be an elusive goal.
Accordingly, the next phase of our work concerned generic modelling of the shape of the airway. To do this we adopted the technique of active shape modelling which has previously been investigated in the context of creating brain atlases, active appearance models and models of bone development. Our work focussed on the mandible. We developed a 3D shape model in which the main modes of variation can be visualised in three dimensions and studied. The model, which is controlled by a small number of parameters, was created using CT scans of dry human mandible specimens. One of the ten sets was selected as a base, and the other nine were registered to it. The registration process deforms an image set so that it matches the base set. The correspondence of between each surface point of and image set and the base image set can then be found. The surface geometry of the base image set was encoded as a set of triangles that represents the geometry accurately. Each co-ordinate of each vertex of this set is taken as a variable, and principal component analysis is used to find the main modes of variation in the set. The principal components can be used to reconstruct any mandible shape that is a linear combination of the others. The largest mode of variation in the data sets was due to the different sizes of the specimens. However, shape changes, such as elongation could also be observed. Some smaller modes of variation were caused by the shape, position or absence of teeth. To achieve accurate results the teeth had to be removed by hand segmentation.
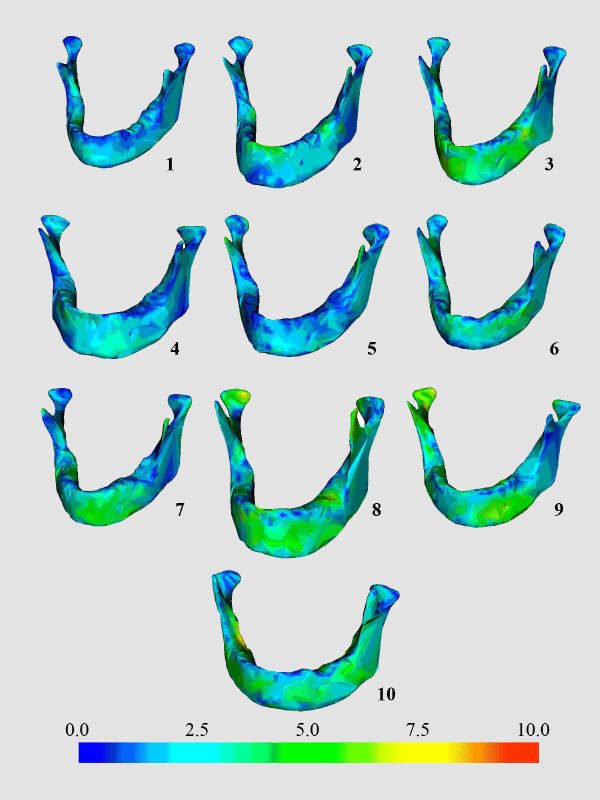 |
Mandible ReconstructionOur generic model of the mandible can be adjusted to match any specific patient's geometry. Here are the results of a study in which it was adjusted to match ten unseen mandibles. Only a small set of bedside measurements were used. The spatial errors between the originalmandible and the closest approximation of the model are colour coded. Mandibles with less accurate reconstruction are outliers of the set uced to create the generic model. The average error at the surface points was normally less than 1.5 mm.The results are from Krista Lam's PhD Thesis (in preparation) |
The work clearly demonstrates the potential of shape models to encode the geometry of the human mandible in a quantitative form suitable for use in accurate simulation of the human airway. In our studies to date we have found that just four principal components are needed to capture the majority of the variance in the set (approximately 94%). This further strengthens the argument that accurate patient specific geometry can be determined from simple bedside measurements.