Both local process names and action names may be indexed. This greatly increases the expressive power of FSP as demonstrated by the following examples.

Buffer

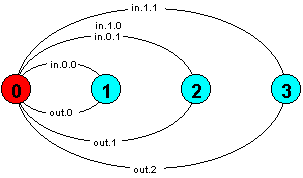
The first example is a single cell buffer which stores integer values in the range 0..2.

BUFFER = EMPTY,
EMPTY  = (in[x:0..2] -> FULL[x]),
FULL[x:0..2] = (out[x] -> EMPTY).

Initially the buffer is empty until an in action to store a value occurs. This action may be to store the value 0, 1 or 2 as indicated by the range [x:0..2]. The process moves into a state in which it stores the appropriate value FULL[0], FULL[1] or FULL[2]. Outputting the value returns the buffer to the EMPTY state. The scope of the range variable x in each case is the local process in which it is declared. The LTS for the process is depicted below:

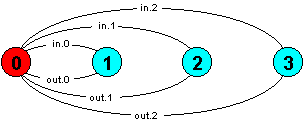
The buffer process can be expressed more succinctly as below. BUF is exactly equivalent to BUF and generates an identical LTS.

BUF = (in[x:0..2] -> out[x] -> BUF).

When modelling behaviour of concurrent systems, it is frequently convenient to think of an action with a range as inputting a value in that range and an action indexed with a variable as outputting the value of that variable.

Range declaration

Ranges may be explicitly declared as shown below:

range T = 0..2
BUF = (in[x:T] -> out[x] -> BUF).

Store Location

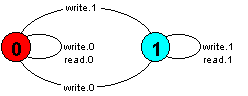
A store location may be modelled as below. To ensure a small LTS, the location stores a single bit:

range BIT = 0..1
STORE = VAL[0],
VAL[b:BIT] = ( write[v:BIT] -> VAL[v] 
              | read[b] -> VAL[b]
              ).

SUM

Both local processes and actions may have more than one index as illustrated by this example (for actions). A process which outputs the sum of two integers (in the range 0..N).

const N = 1
SUM = (in[a:0..N][b:0..N] -> out[a+b] -> SUM).

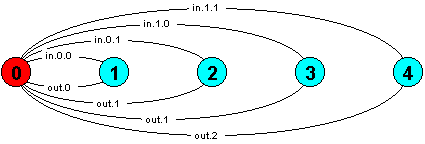
The observant reader will notice that the LTS for SUM is not minimal. The minimal system can be arrived at by minimising using LTSA or redefining SUM as follows:

const N = 1
SUM = (in[a:0..N][b:0..N] -> TOTAL[a+b]),
TOTAL[s:0..2*N] = (out[s] -> SUM).