Figure 1
ic.doc.ltsa.HPWindow. The tool requires jcommon and
jfreechart JARs to be in the classpath, available from
http://www.object-refinery.com.
The versions used with LTSA can be dowloaded from here
jfreechart-0.8.1.jar and
jcommon-0.6.1.jar
This section briefly describes the features that have been added to the FSP language. Grammar rules for the extended form of FSP are given in a separate document. Features added to the tool to support these language features are described in the next section.
FSP now includes floating-point expressions, necessary for
specifying probabilities and distribution
parameters. Floating-point expressions have the expected form, and
can only appear in certain places. In general, a floating-point
expression cannot appear wherever a normal expression
can. Floating-point constants can be defined using the syntax
float IDENTIFIER = FloatingPointExpression.
Processes can be given floating-point parameters in addition to normal parameters. The type of parameter in the process declaration is inferred at compilation time by its default value, and types must agree in all subsequent process references. A floating-point parameter must therefore be given a default value that is unambiguously a floating-point value, either by referring to floating-point constants or by specifying a floating-point literal (e.g. 1.0 instead of 1). Floating-point parameters can be accessed in the same way as normal parameters, but can only be referenced from within floating-point expressions.
Within a process, a transition can set a clock and then wait on that clock to expire. This is the fundamental mechanism that allows simulation to occur. When a clock is set with some value, it takes that value and then proceeds to run down to zero at a uniform rate. When a clock reaches zero, it is said to have expired. All clocks in a simulation run at the same rate (subject to hold and resume). It is possible to guard a transition with a test such that a transition can only be made when a set of clocks have expired (it is also possible to specify that a clock has not expired). The initial value of a clock is zero.
The syntax for setting a clock is e
<c:dist(params)> -> P, meaning that the process
can transit with event e, setting clock c to a value taken from
the given distribution. A table of distribution types and their
parameters can be found in the grammar specification that
accompanies this page. It is possible to specify multiple actions
to occur with a transition as a comma-separated list between the
angle brackets.
The syntax for guarding a transition is ?c? e ->
P, meaning that the transition occurring with event e is
only available when clock c has expired. To state that a
transition is only available when a clock has not expired, the
condition is written !c as opposed to
c. Again, multiple conditions can be placed on a
transition by giving them as a comma-separated list between the
'?' marks. The example in the Clock Holding section of this page
illustrates setting and testing of clocks.
A mechanism has been implemented such that it is possible to
stop a clock running and later start it again. This feature is
essential for modelling certain situations, such as pre-emptive
scheduling. Syntactically, a clock c is held by the term
c:hold within a clock setting block, and is resumed
with c:resume. A pre-emptive system is shown in the
example below:
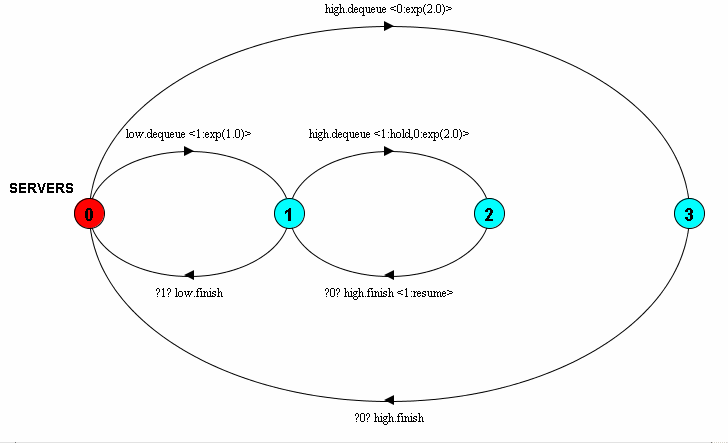
SERVER(MU=1.0) = ( dequeue <c:exp(MU)> -> RUNNING
| interrupt -> continue -> SERVER ),
RUNNING = ( ?c? finish -> SERVER
| interrupt <c:hold> -> INTERRUPTED ),
INTERRUPTED = ( continue <c:resume> -> RUNNING ).
NO_INTERRUPT = STOP + {interrupt, continue}.
||SERVERS(HIGH=2.0,LOW=1.0) = ( high:SERVER(HIGH) || low:SERVER(LOW)
|| high:NO_INTERRUPT )
/ { high.dequeue/low.interrupt, high.finish/low.continue } .
The specification describes a SERVER process that starts its service with a dequeue action, and after some time completes it with a finish action. Whilst in service, the interrupt action can cause the server to suspend its processing, holding its service time clock. The continue action allows the service time clock to resume, and so service can continue.
The system overall describes two of these servers configured in
such a way that when one server (the high priority server) starts
a service it interrupts the other server, allowing it to continue
when the high priority server completes its service. The process
NO_INTERRUPT serves to prevent the high priority
server from engaging in the interrupt or continue actions. The
resulting transition system is shown below:
The probabilistic choice operator allows the user to specify that a process will behave in a number of ways according to some probability weighting. An example of this operator in use is given below:
CHANNEL(E=0.2) = (in -> CH),
CH = ( (1 - E) (out -> CHANNEL)
| (E) CHANNEL ).
The example shows a noisy communication channel, which may lose
a message with probability E. The sub-process CH uses
probabilistic choice to specify the behaviour that following an in
action, it will perform an out action with probability 1-E, or
return to its initial state with probability E. The transition
system this specification produces is shown in Figure 2.
There are three types of measure defined for use with simulation of models. These are a counter for recording the number of occurrences of events in the model, a system-measure for recording the state of some internal variable during the course of simulation and a timer for recording the time between pairs of events. The example below defines each of these measures:
counter P {a, b, c}
measure Q <a, b>
timer R <a, b>
timer S { <a, b>, forall[i:0..10] <c[i], d[i]> }
P is a counter that will record the number of occurrences of the events a, b and c.
Q is a system measure. It is specified using two sets of events (note that while these are singletons in the example, they can also be any set of events defined in the usual manner). The first set of events are those that will increment the value of the internally maintained variable. The second will decrement the variable. The variables initial value is 0. This type of measure is commonly used for recording the population of a system (with increment events being those that indicate an arrival to the system, and decrement events those that indicate a departure), and utilisation of a server (with increment event being that which occurs when service starts, the decrement event that which occurs when service completes).
R is a simple timer. It specifies a single pair of events. The first event is the event that will start the timer, the second event is that which will stop the timer. When the start event occurs, the current simulation time is recorded and placed into a FIFO queue. When the stop event occurs, the time at the front of this queue is removed, and the difference between the current simulation time and that time recorded. In this way the time is implicitly FIFO, and will accurately record the times spent in a FIFO system by jobs (for example, by setting the start event to be that of an arrival to the system, and the stop event to be that of a departure).
More complex forms of the timer can be created, as seen in S. Here, we can define several pairs of events. Each pair of events corresponds to a separate queue in the timer for maintaining samples. The start event in each pair will place the current time in the appropriate queue, the stop event will remove that time from the appropriate queue. Note that it is possible to specify a large range of these pairs using a forall construct. This timer can be used to accurately record the times spent in a non-FIFO system. To achieve this, the notion of job identities is required, so that a job enters the system with some event indexed with its identity, and leaves with another event indexed by its identity. Measures are used in a simulation by composing them with the system to be simulated. Results are available after the simulation has completed.
Within the LTSA tool, in the 'Options' menu is an item 'Use simulation features'. This item governs how composition is performed and what features within LTSA are available.
When selected, composition is performed such that actions and conditions are correctly transferred to the resultant system. Also, probabilistic transitions are composed with respect to the semantics that probabilistic transitions have the highest priority and the semantics of probabilistic composition described in my earlier report. Parsing is unaffected by the state of the 'Use simulation features' item.
When the 'Use simulation features' is not selected, all features of LTSA are available (such as minimise, check safety, partial order reduction) with the exception of simulation. When the item is selected, simulation becomes available, however minimisation and partial order reduction are disabled, as these features are not compatible with extended systems. Property checking is available regardless of whether 'Use simulation features' is selected, and occurs with respect to the correct composition.
Batch management allows the user to either perform a single run of a simulation or to perform multiple runs (batch) of the simulation to obtain confidence intervals. All batch management options are presented in the 'Batch Management' section of simulation options (see Figure 3).
Whether a single run or batch of runs is performed is determined by selecting the appropriate option. When a batch is chosen, the user can specify the number of degrees of freedom to produce for confidence intervals and the confidence level. 'Degrees of freedom' controls the number of runs that are performed (number of runs is degrees of freedom plus one). Using more degrees of freedom produces tighter confidence intervals though clearly requires more execution time. Valid values for degrees of freedom are integers 1 and above. 'Confidence level' determines statistically how strong the confidence intervals are. Valid values are between 0 and 1. Confidence intervals are calculated using Student's T-distribution.
All options for controlling what graphs are produced and how they are displayed are given in the 'Graphing' section of simulation options.
It is possible to specify what type of data should be recorded in time series graphs of measure values. It is possible to choose from either a running average or a moving average. The running average plots the mean value of measures since simulation began against time, and should converge over time. The moving average plots the average value of a measure during a window of a certain size.
Regardless of which average type is chosen, the 'Number of sample points' parameter determines how many times during simulation measures are sampled for charting. Sampling occurs at equal intervals. Note that during simulation progress not all sample points are displayed for reasons of efficiency. When a moving average graph type is selected, the 'Moving average period' parameters determines the size of the window for calculating the moving average, in terms of number of sample points. Note that when a moving average plot is used, a period at the beginning of a plot (corresponding to the size of the moving average window) will be left blank as not enough data exists to draw points there.
The measures that are plotted during simulation progress can be selected from the 'Select measures to show during progress' list. This is for reasons of clarity. Regardless of which measures are plotted during progress, graphs for all chartable performance measures are available in the results.
Histograms can be produced to show the distributions of timer and counter measure types. Histograms are configured in the 'Histogram bounds' section of simulation options. A list of all the measures from which histograms may be produced is presented on the left. When one of these measures is selected, a panel on the right shows the parameters for that measure.
'Make histogram' determines whether histograms will be produced for that measure. 'Number of buckets' specifies how many buckets the histogram will possess, i.e. how many categories. 'Minimum value' and 'Maximum value' specify the lower and upper bounds of the histogram. The range of values between these will fall into one of the specified number of categories, which all have equal width. Values outside this range will be recorded as underflows and overflows.
A histogram is produced for each chosen measure for each run of the simulation in a batch.
Data produced during simulation can be exported in several ways. Firstly, the statistical summary data produced can be copied to the system clipboard. Similarly, the histogram data produced can be copied to the clipboard. This is achieved by right-clicking on the statistical summary to produce a pop-up menu presenting options to 'Copy statistics' and 'Copy histogram data'.
The charts produced can be saved or printed. Right-clicking on a chart produces a pop-up menu presenting these options. Properties of the chart such as background colour can also be altered via this menu.
As can be seen in Figure 1, it is possible to draw the transition system decorated with the conditions and actions associated with each transition. Systems are automatically drawn in this way when 'Use simulation features' is selected. However, a reduced form can be presented by selecting the 'Use V2 label format when drawing LTS' item in the 'Options' menu. In this reduced format, only the events associated with each transition are drawn and the conditions/actions are omitted.
When the system is drawn, clocks are represented not by their text names, but by a numerical identifier. This is done to avoid confusion where the same clock name is used in several process definitions, which refer to separate clocks due to clock identifier scoping.
Clock conditions are represented by a comma-separated list of the clock identifiers (with negation of a condition denoted by prefixing the clock identifier with '!') enclosed within '?' symbols. This appears before the event name associated with the transition. Similarly actions are represented by a comma-separated list enclosed within angle brackets. Actions can be of several types.
A clock setting action is represented by
x:dist(params), where x is a clock identifier, dist
is the distribution type and params are the parameters to that
distribution. Clock holding and clock resume actions are
represented by x:hold and x:resume
respectively, where x is a clock identifier.
Various measurement actions are also
represented. X++ and X-- represent the
increment and decrement of a system-measure X (defined using
measure X <a, b>). X(n).start and
X(n).stop represent start and stop actions (within
timer queue n) for the timer measure X (defined using timer
X {<a,b>,<c,d>} ). Finally, X.e
represents the recording of an event e in the counter measure X
(defined using counter X {a, b, c} ).
Probabilistic transitions are decorated with the probability with which they occur. See Figure 2 for an example.