The aim of the project is to investigate a general clause theorem prover by implementing it in QProlog in two different ways. The prover itself is based on a simple extension to Prolog.
A Horn clause has one of the three forms A, A:-B1 and ... and Bn, or :-B1 and ... and Bn, where the B are atoms. These clauses are, respectively, equivalent to A, A or ~B1 or ... or ~Bn and ~B1 or ... or ~Bn. More generally, a clause will contain more than one positive atom (notice a Horn clause has at most one positive atom) and has the general form A1 or ... or Am or ~B1 or... or ~Bn (0<=m and 0<=n). If m=n=0 the clause is called the empty clause and is equivalent to false.
The aim of a clausal theorem prover is to show that a given set of clauses has no Herbrand model. That is, every assignment of true or false to each atom (or instance of atom) in the clauses will make at least one of the clauses false.
The
motivation for the proposed extension, is illustrated using the following
simple example. Given:
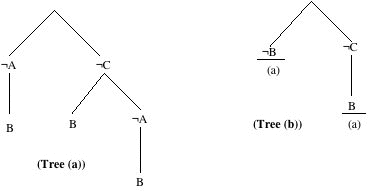
(1) A or B, (2) ~A or B or C, (3) ~A or ~C, (4) ~B or ~C, (5) C or ~B.
Informally, we might argue that these clauses cannot have a model as follows:
Either A or C must be false from (3). Suppose A is false, then B must be true
from (1). On the other hand, if C is false then either A is false or B is true
from (2). If A is false then B must be true from (1). So in all cases B must be
true. Now, either B or C is false from (4). Since B must be true C must be
false. From (5) B must be false, which is not possible. Therefore it is not
possible for all clauses to be true. This reasoning can be set out in tree
form. In (a) below is the reasoning leading to the conclusion that B must be
true and in (b) is the reasoning leading to a contradiction.

The trees in Figures (a) and (b) are very similar to execution trees of a logic program and this is the key to the method. If, for the moment, you ignore the atom B in clauses (1) and (2) they become Horn clauses and the tree in (a) is exactly the proof tree for the query "show A and C". Introducing B back into clauses (1) and (2) the proof tree can be viewed as a proof of the clause B or B, which is equivalent to B. The tree in (b) is the proof tree for "show B and C", where B is treated as a fact.
A theorem prover for arbitrary clauses using this approach uses the following steps.
Every tree must begin with a clause containing no positive literals.
In each clause with more than one positive literal, one positive literal is selected and called the conclusion. All other positive literals, such as B in clauses (1) and (2), are called lemma literals and are treated as B was in the example. That is, they will initially be ignored when completing the tree.
Each leaf node (labelled by a negative literal) can be extended by a clause with a matching conclusion literal. If there are no negative literals in the extending clause the branch is terminated. Otherwse, the negative literals in the extending clause must be further extended, until all branches are terminated. The lemma literals of the clauses used for extension are collected to form a clause called a lemma (effectively the tree is a derivation of this clause) which is added to the program, after first applying the rule (Select) if there are more than one positive literal. Thus if the lemma literals were A1, ..., An, the clause would be A1 or ... or An. If there are no lemma literals to be collected the tree is closed and represents the derivation of the empty clause.
To avoid generating trees of large depth, the depth is controlled, with all trees of upto a given length k being formed and any lemmas derived. In turn, these lemmas may be used to keep the depth of any tree under k. Only when no more steps can be made within depth k is the depth increased. Note that, although the example illustrated was ground, it turns out to be very easy to deal with general literals such as A(x,y,f(a)).)
The project is to write a prover in QProlog implementing the above strategy. The prover should be tested on problems from the database TPTP (Thousands of Problems for Theorem Provers).
Some helpful hints will be given to any group that chooses this project In particular, there are two ways to implement the prover. The first (more standard) way is to write an interpreter. The second way is to exploit the similarity of the strategy with Prolog and partially compile the data into a Prolog program. An easy case is when all clauses are Horn clauses, for then the compiled version will run exactly as Prolog. One idea is to include as an extra argument in the conclusion literal of a clause the list of lemma literals, which are accumulated as each clause is used in a derivation. On terminating a tree these literals wil be processed and a new clause added to the program.