One of the most important concepts in number theory is the notion of a prime number. A natural number n is prime if n ≥ 2 and the only divisors of n are n and 1. An integer n ≥ 2 that is not prime is composite. Note that the number 1 is by definition not a prime number, so the smallest prime number is 2. And 2 is the only even prime number because by definition all even numbers are divisible by 2.
A fundamental theorem in number theory states that every integer n ≥ 2 can be factored into a product of prime powers. This factorisation is unique in the sense that any two such factorisations differ only in the order in which the primes are written. For example:
12 = 22*3
5 = 5
15000 = 23*3*54
123456789 = 32*3607*3803
Although it seems easy to factor an integer, it is actually not always. Generally, if the number has only small factors, then it is not hard to factor. But if the number is very large and has only a few large factors, then there is no efficient algorithm currently available. The most efficient classical algorithm known for factoring integers larger than 100 digits is the general number field sieve (GNFS). Its time complexity is sub-exponential, i.e. put informally it runs in time greater than polynomial time, but less than exponential time. Under some reasonable heuristic assumptions, the GNFS method factors n in time:
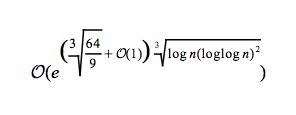
If n is large, then it will take a long time to factor it. For example, in 2005, a research team factored a 193 decimal digits (640-bit) number which has two large prime factors. The effort took approximately 30 2.2GHz-Opteron-CPU years, over five months of calendar time. The presumed difficulty of this problem is at the heart of certain algorithms in cryptography such as RSA. However, since there exists a factorisation algorithm which is sub-exponential, RSA is easier to break comparing to well-designed symmetric-key algorithms when they have the same key size. That's why you need longer keys in RSA. Here is a table comparing the key sizes to achieve the same security level:
| RSA | Symmetric-key Algorithm |
| 1024-bit | 80-bit |
| 2048-bit | 112-bit |
| 3072-bit | 128-bit |
| 7680-bit | 192-bit |
| 15360-bit | 256-bit |
There does exist a polynomial-time factorisation algorithm, Shor's algorithm. It runs in O((log n)3) time. However, this algorithm can only run on a quantum computer. Currently quantum computers are quite primitive and the largest number has ever been factored using Shor's algorithm is 15. It may take years before we can use it for large numbers.
Useful Links