Sometimes, a finite field is also called a Galois Field. It is so named in honour of Évariste Galois, a French mathematician. Galois is the first one who established the following fundamental theorem on the existence of finite fields:
An order-n finite field exists if and only if n = pm for some prime p (p is called the characteristic of this finite field) and some positive integer m.
In fact, an order-n finite field is unique (up to isomorphism). All finite fields of the same order are structurally identical. We usually use GF(pm) to represent the finite field of order pm. As we have shown above, addition and multiplication modulo a prime number p form a finite field. The order of the field is p1. However, modulo arithmetic on its own will not let us to construct a finite field with order of pm for m > 1. For example, 23 = 8, and we've already know (Z8, +, *) is not a field. One way to construct a finite field with m >1 is using the polynomial basis. The field is constructed as a set of pm polynomials along with two polynomial operations.
Here a polynomial f(x) is a mathematical expression in the form anxn + an-1xn-1 + ... + a0. The highest exponent of x is the degree of the polynomial. For example, the degree of x5 + 3x3 + 4 is 5. In a polynomial, an, an-1, ... , a0 are called coefficients. If in a polynomial, the coefficients an, an-1, ... , a1 are all 0, or in other words, the polynomial is in the form of a0, we call this polynomial a constant. We can add, subtract polynomials by combine the terms in the polynomials with the same powers. For example:
Polynomial addition: (x5 + 3x3 + 4)+(6x6 + 4x3) = 6x6 + x5 + 7x3 + 4
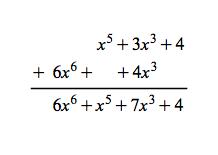
Polynomial subtraction: (x5 + 3x3 + 4)-(6x6 + 4x3) = -6x6 + x5 -x3 + 4
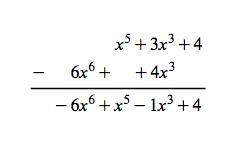
We can also multiply two polynomials. The general rule is that each term in the first polynomial has to multiply each term in the second polynomial, then sum the resulted polynomials up. For example:
Polynomial multiplication: (x5 + 3x3 + 4)*(6x6 + 4x3) = 6x11 + 18x9 + 4x8 + 36x6 + 16x3
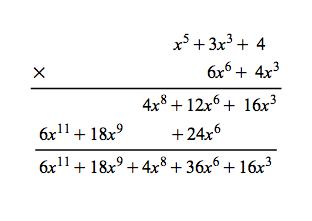
We can also divide polynomials using long division. For example:
Polynomial division: (6x11 + 18x9 + 4x8 + 36x6 + 16x3) ÷ (x5 + 3x3 + 4) = 6x6 + 4x3
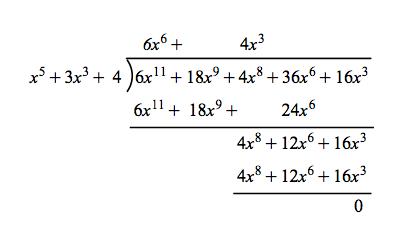
But in many cases the divisors cannot divide the dividends, which means you will have remainders. For example:
Polynomial division with remainder: (3x6 + 7x4 + 4x3 + 5) ÷ (x4 + 3x3 + 4) = 3x2 - 9x + 34 with remainder -98x3 - 12x2 + 26x -131
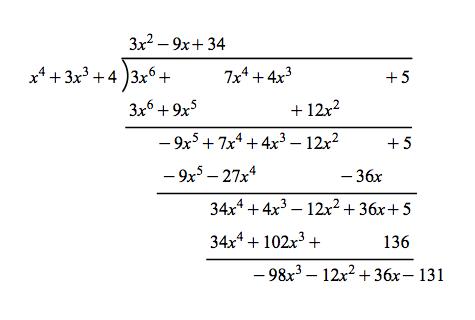
If a polynomial is divisible only by itself and constants, then we call this polynomial an irreducible polynomial. We will see later that irreducible polynomials have properties similar to prime numbers.
If the coefficients are taken from a field F, then we say it is a polynomial over F. With polynomials over field GF(p), you can add and multiply polynomials just like you have always done but the coefficients need to be reduced modulo p. For example, compare the above results with polynomials over GF(11):
(x5 + 3x3 + 4)+(6x6 + 4x3) = 6x6 + x5 + 7x3 + 4
(x5 + 3x3 + 4)-(6x6 + 4x3) = 5x6 + x5 +10x3 + 4
(x5 + 3x3 + 4)*(6x6 + 4x3) = 6x11 + 7x9 + 4x8 + 3x6 + 5x3
(3x6 + 7x4 + 4x3 + 5) ÷ (x4 + 3x3 + 4) = 3x2 + 3x + 3 with remainder x3 + 10x2 + 4x +1
Similar to integers, you can do modular arithmetic with polynomials over a field. Now the operands and modulus are polynomials. Let f(x)= anxn + an-1xn-1 + ... + a0 and g(x)= bmxm + bm-1xm-1 + ... + b0 be two polynomials over a field F, then there is a unique polynomial r(x) of degree smaller than m and another unique polynomial h(x), both over F, such that f(x) = h(x)*g(x)+r(x). The polynomial r(x) is called the remainder of f(x) modulo g(x). For polynomials a(x), b(x) and g(x) which are over the same field, we say a(x) is congruent to b(x) modulo g(x) written a(x) ≡ b(x) mod g(x), if m(x) divides a(x)-b(x). For example (all polynomials are over GF(3)):
2x2 ≡ 2 mod (x2-1)
x4 ≡ 1 mod (x2-1)
x3 ≡ x mod (x2-1)
2x2+x4 ≡ 0 mod (x2-1)
2x2*x4 ≡ 2 mod (x2-1)
2x2+x3≡ x +2 mod (x2-1)
Always remember there are two moduli involved: a polynomial modulus and an integer modulus. You need to reduce the result from the polynomial operations by modulo the polynomial modulus and then reduce the coefficients modulo the integer modulus. Take one of the above examples: 2x2+x4= x4+2x2, you reduce this result by dividing by x2-1:
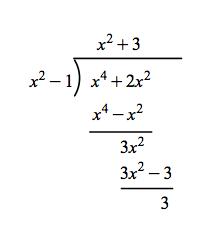
The remainder 3 is then reduced modulo 3: 3 ≡ 0 mod 3. So the final result is 2x2+x4 ≡ 0 mod (x2-1).
Useful Links