A vector pipeline processor is an extension to a conventional CPU, which
provides registers which can hold an entire vector of floating-point
operands (e.g. 64 words). In addition, the machine would have
instructions which manipulate vectors. For example, to implement the
following loop:
for i := 1 to 64 do
for j := 1 to 64 do
Y[k,j] := a * X[i,j] + Y[k,j];
This could be programmed as follows:
R1 := 0
R2 := 0
R3 := k*N
for i := 1 to 64 do
LV V2,X(R1) ; load row of X (R1 is i*N, where N is row length)
MULTSV V3,a,V2 ; multiply each element of the row vector by scalar 'a'
LV V1,Y(R2) ; load k'th row of Y, where R2 is k*N)
ADDV V4,V3,V1 ; add Y[i] and a*X[i]
SV V4,Y(R3) ; store the vector into array Y
R1 := R1+N
R2 := R2+N
end do
The classic vector pipeline machine is the Cray 1, and there are many
later designs from Cray and others (eg the NEC SX-6 used in the Earth Simulator). The main advantages of vector registers and vector
instructions are that pipelined floating point arithmetic can be
organised very efficiently, and the maximum throughput of a
highly-interleaved memory system can be exploited.
We will study vector processors in more detail shortly. No further
details are needed for this exercise.
This exercise concerns Amdahl's Law, which is discussed at length in
the textbook:
Assume that we are considering accelerating a machine by adding a vector mode
to it. When a computation is run in vector mode, it is 20 times faster than
the normal mode of execution. We call the percentage of time that could be
spent using vector mode the percentage of vectorisation.
- What percentage of vectorisation is needed to achieve a speedup of
2?
- What percentage vectorisation is needed to achieve one-half the maximum speedup
available from using vector mode?
- Suppose you have measured the percentage of vectorisation for
programs to be 70%. The hardware design group says they can double the
the speed of the vector mode with a significant engineering investment.
You wonder whether the compiler crew could increase the use of vector
mode as another approach to increasing performance. How much of an
increase in the percentage of vectorisation (relatitive to current usage)
would you need to obtain the same performance gain? Which investment would
you recommend?
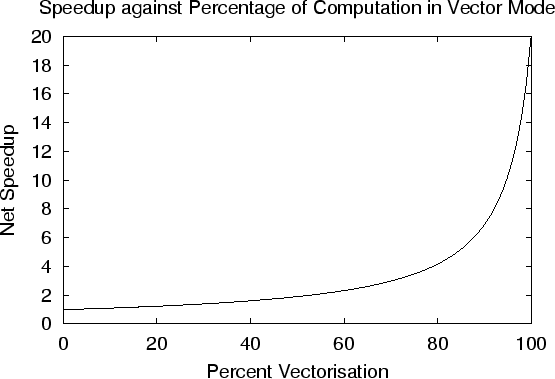
- Draw (sketch!) a graph which plots the speedup as a percentage of the
computation performed in vector mode. Label the
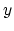 axis ``Net Speedup'',
and label the
axis ``Net Speedup'',
and label the 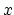 axis ``Percent Vectorisation''.
axis ``Percent Vectorisation''.
(each part should take only a few minutes; you do not really need
a calculator to uncover the basic point of this exercise -
back-of-the-envelope estimates are quite adequate).
Assume that we make an enhancement to a computer that improves some
mode of execution by a factor of 10. Enhanced mode is used 50% of
the time, measured as a percentage of the execution time when the
enhanced mode is in use (rather than as defined in the notes,
where the percentage of the running time without the enhancement
is used).
- What is the speedup we have obtained from fast mode?
- What percentage of the original execution time has been
converted to fast mode?
(These exercises are taken from Hennessy and Patterson).
Paul Kelly, Imperial College, 2007
- For net speedup of 2, we need
Rearranging Amdahl's Law gives:
So
- With the original vector mode design, 70% vectorisation yields a
net speedup of
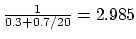 . Increasing the
vector mode speedup to a factor of 40 would increase this to
. Increasing the
vector mode speedup to a factor of 40 would increase this to
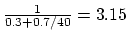 .
.
To achieve this net speedup by improving the compiler, we must increase
the percentage vectorisation. We have
Rearranging as before, we get
So the compiler crew only have to do a couple of percent better to
outperform the proposed hardware development.
- To sketch this graph consider a few points, e.g.
- when the percentage vectorised is 0%, net speedup is 1.
- when the percentage vectorised is 100%, net speedup is 20.
- when the percentage vectorised is 50%, net speedup is
- when the percentage vectorised is 75%, net speedup is
- To compute the speedup obtained from the fast mode we must work out the execution time
without the enhancement. We know that the accelerated execution time
consisted of two halves: the unaccelerated phase (50%) and the accelerated
phase (50%).
Without the enhancement, the unaccelerated phase would have taken just as
long (50%), but the accelerated phase would take 10 times as long, i.e.
500%. So the relative execution time without the enhancement would
be
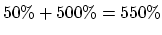 .
.
Thus the overall speedup is
- To find the percentage of the original execution time which
was accelerated, we plug these figures into Amdahl's Law again:
Paul Kelly, Imperial College, 2007





![]() .
.
