A new computer is to be built using a DLX CPU. Trace-driven
simulation of a set of programs gave the following results:
Table 1:
Miss-rates for unified caches
|
| Cache size |
Assoc. |
Tot miss rate |
Compulsory |
|
Capacity |
|
Conflict |
|
| 32 KB |
2-way |
0.041 |
0.009 |
22% |
0.028 |
68% |
0.004 |
11% |
| 64 KB |
4-way |
0.028 |
0.009 |
32% |
0.019 |
68% |
0.000 |
0% |
| 128 KB |
1-way |
0.026 |
0.009 |
34% |
0.004 |
16% |
0.013 |
50% |
|
Table 2:
Miss-rates for instruction-only, data-only and unified
caches (2-way set-associativity)
|
| Cache size |
Instrn. only. |
Data only |
Unified |
| 32 KB |
2.2% |
4.0% |
4.1% |
| 64 KB |
1.4% |
2.8% |
2.9% |
| 128 KB |
1.0% |
2.1% |
1.9% |
|
Assume the following:
- Clock cycle time is 20ns
- Miss penalty is 12 clock cycles
- A perfect write buffer is used that never stalls the CPU
(i.e. the CPU continues as soon as the write is issued)
- The base CPI assuming a perfect memory system is 1.5
- A unified cache adds 1 extra cycle to each load and store
(since there is only a single memory port)
- 26% of instructions involve data transfer
You are considering three options:
- A:
- A 4-way set-associative unified cache of 64 KB
- B:
- Two 2-way set-associative caches of 32 KB each, one for
instructions and one for data
- C:
- A direct-mapped unified cache of 128 KB. Assume that the clock
rate is 10% faster in this case since the mapping is direct and the
CPU address does not need to drive two caches, nor does the data bus
need to be multiplexed. This faster clock rate increases the miss
penalty to 13 clock cycles
- 1.
- What is the average CPI for each
of the three cache organisations?
- 2.
- What cache organisation gives best average performance?
- 3.
- Sketch a program for which each scheme gives the worst
performance
- 4.
- Suppose that the base CPI (assuming a perfect memory system) is
5. How well do options A and C perform?
(These exercises are based on Hennessy and Patterson, first edition, Exercise 8.5).
Paul Kelly and Andrew Bennett, Imperial College, 1999.
It is convenient to divide the execution time of the program into
several components in order to calculate the total CPI. The total CPI
is the sum of these four items:
- 1.
- Base CPI - cycles used by the program operating on an ideal
memory system
- 2.
- Extra cycles required for loads and stores with a unified cache
- each load and store requires one extra cycle (see assumptions above)
- 3.
- Extra cycles for cache misses due to instruction fetches
- 4.
- Extra cycles for cache misses due to data accesses
Components 3 and 4 above are dependent on the miss rate and penalty:
i.e.
Cache configuration A:
- The base CPI is 1.5
- One extra cycle is required for each load and store, defined to
be 26% of instructions, i.e. the second component of the CPI is 0.26
- Extra cycles due to instruction misses: Table 1 shows that the
miss rate for this cache is 0.028, the miss penalty is 12 cycles,
and 1 access is required per instruction. So
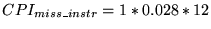
- Extra cycles due to data misses: miss rate and penalty as for
instructions. 26% of instructions are loads or stores, so 0.26
accesses/instruction. So
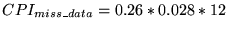
- Summing these three components yields
CPItotal = 2.18
Cache configuration B:
- Base CPI 1.5
- Component 2 is zero, since separate instruction and data caches
are used
- For component 3, Table 2 shows a miss rate of
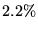 ,
so
,
so
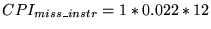
- For component 4, Table 2 shows a miss rate of
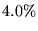 ,
so
,
so
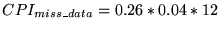
- Summing these three components yields
CPItotal = 1.89
Cache configuration C:
- Base CPI 1.5
- Component 2 is 0.26 (as configuration A)
- For component 3, Table 1 shows a miss rate of 0.026, and the
miss penalty has increased by one cycle so
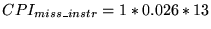
- For component 4,
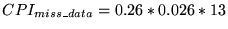
- Summing these three components yields
CPItotal = 2.19
Cache configuration B gives the best CPI.
The cycle time, which varies between cache configuration, must be
taken into account to determine which has the best performance.
Multiplying the total CPIs derived above by cycle time for each
configuration (20ns, 20ns and 18ns) gives A:43.7ns/instruction,
B: 37.8ns/instruction, C: 39.3ns/instruction
Configuration B gives best performance. C is worse,
despite being much larger in size: the extra overhead of the unified
cache, the increased miss penalty, and limited associativity all
outweigh the advantage of using a larger cache.
The differing sizes and associativities of the caches can be used to
construct programs which perform badly in each case. A tight loop
which accesses several arrays is used. The arrays are allocated so
that each is cached into the same cache blocks, and references are
made to each array in turn, causing conflicts. Similarly, several
procedures are required which also map to the same cache blocks.
Configuration C has the lowest associativity, and is therefore
easiest to deal with: it can be made to perform badly by using two
arrays which map to the same blocks. Since it is direct mapped,
accesses to the arrays will be misses due to replacements. The other
configurations will perform better due their greater associativity.
The small size of configuration B can be used to make it the
slowest. Three arrays are required since it is 2-way set associative
- they must be allocated so that they map to the same cache blocks
only on configuration B, so that no conflicts occur on the
other, larger caches.
To make A the slowest requires two procedures which also map
onto the same cache blocks as the arrays.
Replacing base CPI in the expressions in answer 1 gives:
- A:
CPItotal = 5.68
- B:
CPItotal = 5.39
- C:
CPItotal = 5.69
Multiplying by the appropriate cycle time gives:
- A: 113.6ns/instruction
- B: 107.8ns/instruction
- C: 102.3ns/instruction
C is the now the fastest configuration: the improved cycle time
leads to the best performance when the CPI is so high.
Paul Kelly and Andrew Bennett, Imperial College, 1999.