332 Advanced Computer Architecture

Tutorial exercise 8

Introduction: vectorisation

The dependence analysis techniques used in restructuring compilers were originally developed for vector supercomputers, the most successful early example being the CRAY-1. These ``vector pipeline'' machines have a conventional pipelined floating point system, augmented with vector registers V0-V7 - holding up to 64 words each. The instruction set is extended with vector instructions, e.g.

  ADDV  V1, V2, V3      V1[i] := V2 [I] + V3 [i]
  ADDSV V1, F0, V2      V1[i] := F0 + V2 [i]
  LV    V1, R1          V1[i] := Store[R1 + i]
  SV    R1, V1          Store[R1 + i] := V1 [I]

Vector instructions normally operate on all 64 vector register elements (actually a special ``vector length'' register, VLR, controls how many operations are actually done).

Example: DAXPY/SAXPY

The inner-most loop in Gauss elimination is

  for i := 0 to 63 do
    Y [i] := a x X [i] + Y [i]

Gauss elimination is an important application and also a favourite benchmark. If we assume that the starting addresses for X and Y are in Rx and Ry respectively, we can code the loop as:

  LD      F0, a                         load scalar a
  LV      V1, Rx                        load  vector X
  MULTSV  V2, F0, V1                    a (scalar) x X (vector)
  LV      V3, Ry                        load vector Y
  ADDV    V4, V2, V3                    vector + vector
  SV      Ry, V4                        store the result

The feature which makes vector pipeline machines really important is their ability to cope with non-unit stride; the instructions to do this are:

  LVWS  V1, (R1,R2)     for i = 0 to 63 
                          V1[i] := Store[R1 + R2*i]

  SVWS  (R1,R2), V1     for i = 0 to 63 
                          Store[R1 + R2*i] := V1 [i]

Vector machines implement this efficiently using large numbers of parallel memory banks. Caching, even with large blocks, doesn't help. Performance can still, of course, be improved dramatically by reusing values from vector registers instead of rereading them.

Fortran 90 notation for vector operations

To avoid low-level details in the remainder of this exercise, use a high-level notation (borrowed from Fortran 90; the semantics are that the entire RHS is evaluated before assigning to the LHS):

A[1:100] := B[1:100] + C[1:100]*2  for i = 1 to 100
                                     A[i] := B[i] + C[i]*2

A[1:100:2] := A[0:99:2]            for i = 1 to 100 step 2
                                     A[i] := A[i-1]

M1[1:100,1] := M2[1,1:100]         for i = 1 to 100
                                     M[i,1] := M[1,i]

Exercise 8.1. Dependence analysis and vectorisation

For each of the following loops, find all the dependences (you may find it useful to show them as arrows connecting the statements of the loop), and if possible write down a vectorised version with the same input-output behaviour:

for i := 1 to N do
  A[i] := A[i] + B[i-1];

for i := 1 to N do
  A[i+1] := A[i] + 1;

for i := 1 to N step 2 do
  A[i] := A[i-1] + A[i];

for i := 1 to 10 do
  A[10*i] := A[11*i]

for i := 1 to N do
  A[i] := B[i];
  C[i] := A[i] + B[i];
  E[i] := C[i+1];

for i := 1 to N do
  A[i] := A[i] + A[i+1];

(is there a problem with this?)

for i := 1 to N do
  A[i] := B[i];
  C[i] := A[i] + B[i-1];
  E[i] := C[i+1];
  B[i] := C[i] + 2;

(30%) Index set splitting is a transformation in which a loop is split into two parts, so that in the range where no dependency occurs vectorisation can be applied.
Apply index set splitting to the following loop, and show how it can be vectorised:
```
for i := 1 to 200 do
  B[i] := B[i] + B[200-i];
```

Exercise 8.2. Computing a running total

Assuming (this is a hint!) that N is a power of two (i.e. ${\tt N} = 2^k$ ), write a vectorisable program to compute the same result as the following:

A[1] := B[1];
for i := 2 to N
  A[i] := A[i-1] + B[i];

Paul Kelly, Imperial College, 2009

Notes on the solutions to Exercise 8

Exercise 8.1

for i := 1 to N do
  A[i] := A[i] + B[i-1];

There are no dependences here, and the loop is easily vectorised:

A[1:N] := A[1:N] + B[0:N-1]

```
for i := 1 to N do
  A[i+1] := A[i] + 1;
```
The element of A used in each iteration is (except for when i = 1) the value generated in the previous iteration -- so there is a loop-carried data dependence ( $\delta_<$ ) from the statement to itself. The loop is very similar to (and has the same dependence graph as):
```
for i := 1 to N do
  A[i] := A[i-1] + 1;
```
Because of this loop-carried data dependence, there is no parallelism present and no vectorisation is possible. Note, though, that it is possible to recognise the loop as a recurrence and use an algorithm like the one is question 8.3.
```
for i := 1 to N step 2 do
  A[i] := A[i-1] + A[i];
```
In this case there is no data dependence: both references to A are intended to refer to the old values before the loop started. There is no anti-dependence either, since there is no danger that the assignment might destroy a value before it is used.
```
for i := 1 to 10 do
  A[10*i] := A[11*i]
```
The question here is whether the left and right-hand sides ever refer to the same array element, that is when . There are many solutions, but we are only interested in integer values of the loop control variable. You can see by enumerating the values of the subscript expressions that this happens for , , , etc. All of these solutions lie outside the actual range for i, so there is no dependence and we can vectorise:
```
A[10:10*N:10] := A[11:11*N:11]
```
(this illustrates how array assignments with non-unit stride are expressed in Fortran-90).
```
for i := 1 to N do 

 A[i] := B[i]; 

 C[i] := A[i] + B[i]; 

 E[i] := C[i+1]; 
```
We have $S_1 \delta_= S_2$ because of A, and $S_3 \overline{\delta}_< S_2$ because of C (because C[i+1] must be used by before it is destroyed by the instance of in the following iteration.
The dependence graph has no cycles, by indicates that instances of must be executed before instances of , so the vectorised code is:
```
 A[1:N] := B[1:N]; 

 E[1:N] := C[2:N+1]; 

 C[1:N] := A[1:N] + B[1:N]; 
```
```
for i := 1 to N do
  A[i] := A[i] + A[i+1];
```
The dependence graph here shows an anti-dependence ( $\overline{\delta}_<$ ) from the statement to itself, because the element A[i+1] referred to is destroyed in the following iteration. According to our analysis this cycle blocks vector code generation.
However, it is easy to avoid the anti-dependence by taking a copy of A, modifying the code to
```
for i := 1 to N do
  A2[i] := A[i+1];
for i := 1 to N do
  A[i] := A[i] + A2[i];
```
Now both of these statements are vectorisable:
```
A2[1:N] := A[2:N+1]
A[1:N] := A[1:N] + A2[1:N]
```
It turns out that if you look at how this code is represented in DLXV or CRAY assembler, this copying happens as a matter of course when the vector is loaded into a vector register.


for i := 1 to N do

 A[i] := B[i]; 

 C[i] := A[i] + B[i-1]; 

 E[i] := C[i+1]; 

 B[i] := C[i] + 2;

Dependences:


        
Statement






.

.



.
.
.



.

.
.



.
.
.

(30%) Index set splitting is a transformation in which a loop is split into two parts, so that in the range where no dependency occurs vectorisation can be applied.
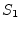
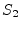
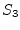
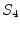
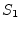
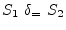
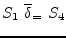
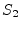
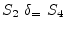
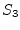
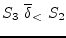
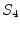
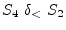
Apply index set splitting to the following loop, and show how it can be vectorised:
```
for i := 1 to 200 do
  B[i] := B[i] + B[200-i];
```
For iterations 1 to 100, the B[200-i] reference is to old data. For iterations 101-200, the B[200-i] reference is to a value generated by an earlier iteration. So split:
```
for i := 1 to 100 do
  B[i] := B[i] + B[200-i];
for i := 101 to 200 do
  B[i] := B[i] + B[200-i];
```
Now, is there a loop-carried dependency? No! The only dependence is between the two now-separate loops. So can we vectorise? Yes - both loops are vectorisable:
```
  B[1:100] := B[1:100] + B[199:100];
  B[101:200] := B[101:200] + B[99:0];
```

Exercise 8.2. Computing a running total

Assuming that N is a power of two (i.e. ${\tt N} = 2^k$ ), write a vectorisable program to compute the same result as the following:

A[1] := B[1];
for i := 2 to N
  A[i] := A[i-1] + B[i];

The loop sets A[i] to be the running total so far, $\sigma_{j=1}^i {\tt B[}i{]}$ . This seems inherently sequential. It turns out that it can be done fairly efficiently in parallel.

One way to think about this is to imagine the full binary reduction tree, to compute each element of A separately. Now, notice that the third element can actually use the result from the second one - there are common sub-expressions.

The trick, then, is to write a program that captures this pattern. Consider the following example, for and B[i] all ones:

Initially:	1	1	1	1	1	1	1	1
Shift by 1		1	1	1	1	1	1	1
Add	1	2	2	2	2	2	2	2
Shift by 2			1	2	2	2	2	2
Add	1	2	3	4	4	4	4	4
Shift by 4					1	2	3	4
Add	1	2	3	4	5	6	7	8

This is implemented as follows, assuming

is a power of 2:

void parallelScan(int R[], int A[])
{
  int i, j, m;
  int T[N]; /* Temporary */
  for (i = 0; i<N;i++) 
    R[i] = A[i];
  for (j = 1; j < N; j*=2) {
    // take a copy of R[0:N-1-j]
    for (i = j; i<N;i++)
      T[i-j] = R[i-j];
    // Now do parallel vector addition R[j:N-1] += R[0:N-1-j]
    for (i = j; i<N;i++)
      R[i] += T[i-j];
  }
}

If you're curious about this, have a look at:

Ladner, R. E. and Fischer, M. J. 1980. Parallel Prefix Computation. J. ACM 27, 4 (Oct. 1980), 831-838. DOI= http://doi.acm.org/10.1145/322217.322232
Chatterjee, S., Blelloch, G. E., and Zagha, M. 1990. Scan primitives for vector computers. In Proceedings of the 1990 Conference on Supercomputing (New York, New York, United States). IEEE Computer Society Press, Los Alamitos, CA, 666-675. http://www.cs.cmu.edu/ guyb/papers/sc90.pdf

It has many interesting applications.

(Paul Kelly, Imperial College, 2009)

Statement
	.	$S_1 \delta_= S_2$	.	$S_1 \overline{\delta}_= S_4$
	.	.	.	$S_2 \delta_= S_4$
	.	$S_3 \overline{\delta}_< S_2$	.	.
	$S_4 \delta_< S_2$	.	.	.