221 Compilers - Exercise 4: Register allocation using graph colouring

Introduction

The idea of using graph colouring for register allocation is covered at the end of Chapter 5 of the lecture notes. However, a good way to understand it is to work through this exercise.

Consider the following sequence of assignments: 

        S1:   A = 100;
        P1:
        S2:   B = 200;
        P2:
        S3:   C = A + B;
        P3:
        S4:   D = A * 2;
        P4:
        S5:   E = B * 2;
        P5:
        S6:   F = D - C;
        P6:
        S7:   G = E + F;
        P7:
We are interested in using registers for all the variables in this code sequence. Notice that we can minimise the number of registers needed by reusing them.

For example, A and F could both be stored in the same register. We don't need a register for F until after the last statement to use A. There are several such instances in this sequence.

Definition: live range

The live range of a variable is the set of program points after which the variable must be safely stored.

Example 1: The live range of A consists of {P1, P2, P3}.

Example 2: The live range of D consists of {P4, P5}

Example 3: The live range of F consists of {P6}.

Subtlety: Can the same register be used for both D and A?

The answer is yes: storage for D is only needed after the value of A has been read. The two live ranges do not intersect.

(as we will see later, A $\in$ liveIn(S4), and D $\in$ liveOut(S4)).

Definition: interference

Two variables interfere if their live ranges overlap.

Example 1: The live ranges of A and F do not overlap.

Example 2: The live ranges of A and B do overlap.

Example 3: The live ranges of A and D do not overlap.

Definition: interference graph

The interference graph for a program consists of

Definition: Colouring

A graph colouring is an assignment of colours to nodes. A graph colouring is valid if no pair of nodes which are linked by an arc carry the same colour.

Exercise 4.1: Simple example

Construct the interference graph for the variables A, B, C, D, E, F and G in the example program fragment above. Colour the graph using the minimum possible number of colours, and use this colouring to assign each variable to a register. Give the final code after register allocation.

Exercise 4.2: Register allocation using graph colouring, real example

Consider the following program fragment: 

        VAR A : ARRAY [0..99] OF INTEGER;

        PROCEDURE P(i, j, size : INTEGER)
        VAR k, tmp : INTEGER;
        BEGIN
          FOR k := 0 TO size-1 DO
            tmp := A[i+k];
            A[i+k] := A[j+k];
            A[j+k] := tmp;
          END
        END

The compiler's intermediate representation of the body of the procedure is as follows: 

                t1 := size-1
                k := 0
        L1:     
                cmp k,t1
                bgt End
                t2 := Address(A)+i
                t3 := t2+k
                tmp := LoadIndirect(t3)
                t4 := Address(A)+j
                t5 := t4+k
                t6 := LoadIndirect(t5)
                StoreIndirect(t6, t3)
                StoreIndirect(tmp, t5)
                k := k+1
                jmp L1
        End:

  1. Construct the register interference graph for the variables t1, t2, t3, t4, t5, t6, k and tmp.

  2. Show how the interference graph colouring algorithm can be used to minimise the number of registers needed in this procedure.

  3. What other possible optimisations are possible in this procedure? Write very brief notes on how such optimisations might be implemented.
Paul Kelly Imperial College October 2011

Exercise 4.2: Register allocation using graph colouring

Sample solutions

Exercise 4.1: Register allocation using graph colouring, simple example

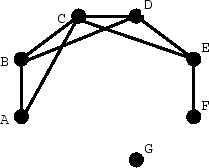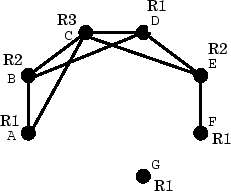\epsfbox{Diagrams/Ex4-SimpleInterferenceGraph.eps}     \epsfbox{Diagrams/Ex4-SimpleInterferenceGraphColoured.eps}
(a) Interference graph   (b) After colouring
Code after register allocation: 
        S1:   A = 100      R1 = 100
        S2:   B = 200      R2 = 200
        S3:   C = A + B    R3 = R1 + R2
        S4:   D = A * 2    R1 = R1 * 2
        S5:   E = B * 2    R2 = R2 * 2
        S6:   F = D - C    R1 = R1 - R3
        S7:   G = E + F    R1 = R2 + R1

Exercise 4.2: Register allocation using graph colouring, real example

  1. Assuming a simple machine with sufficient general-purpose registers, write down straightforward assembly code for procedure P. 
            
        (i coexists with everything
        j coexists with everything
        k coexists with everything)
        t1 coexists with everything
        t2 coexists with t1 (and i,j,k but asked to ignore them).
        t3 coexists with t1,tmp,t4,t5,t6
        tmp coexists with t1,t3,t4,t5,t6
        t4 coexists with t1,tmp,t3
        t5 coexists with t1,t6,t3,tmp
        t6 coexists with t1,t3,tmp,t5

  2. This can be coloured with five registers, e.g. 
            R0: t1
        R1: t2, t3
        R2: t4,t5
        R3: t6
        R4: tmp
    (you also need registers for i, j and k).

  3. t2 and t4 are actually loop invariant, though moving them increases the register pressure. They can be found by computing the set of variables potentially changed in the loop, and intersecting it with the set on which the variable depends. The unconditional jump can be removed from the loop by rotating it. Common subexpressions have already been dealt with.




Paul Kelly Imperial College October 2011

next_inactive up previous