MAGMA: Multi-level Accelerated Gradient Mirror Descent Algorithm for Large Scale Convex Composite Minimization
Motivation
The fidelity in which the optimization model captures the underlying application can often be controlled. Typical examples include the discretization of Partial Differential Equations in computer vision and optimal control, the number of features in machine learning applications, the number of states in a Markov Decision Processes, and so on. In many areas it is common to take advantage of this structure by solving a low fidelity (coarse) model and then use the solution as a starting point in the high fidelity (fine) model.Basic Idea
We adopt a multi-level optimization point of view within accelerated proximal gradient methods and show how to take advantage of the availability of a hierarchy of models in a consistent manner for composite convex optimization. We do not use the coarse model just for the computation of promising starting points but rather for the computation of search directions. The algorithm we propose is similar to the Accelerated Proximal Gradient (APG) class of algorithms. The algorithm we develop combines elements from APG (gradient steps), Mirror Descent (mirror steps), the multigrid framework (coarse correction steps) and smoothing methods (for choosing appropriate step sizes for coarse correction steps). We call the proposed algorithm Multi-level Accelerated Gradient Mirror Descent Algorithm (MAGMA).Theoretical Results
We show that the coarse correction step satisfies a certain descent property and combining it with the mirror descent step with appropriate ste-sizes we show that MAGMA converges to the global minimum with a rate optimal for black-box first-order methods.Numerical Experiments
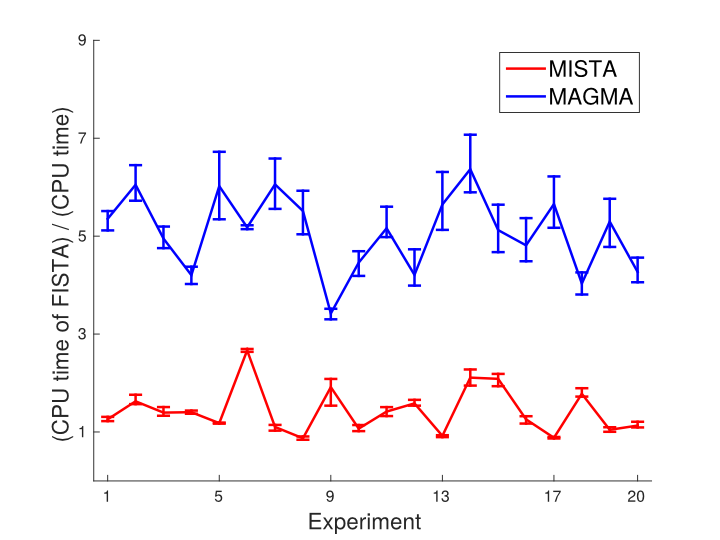
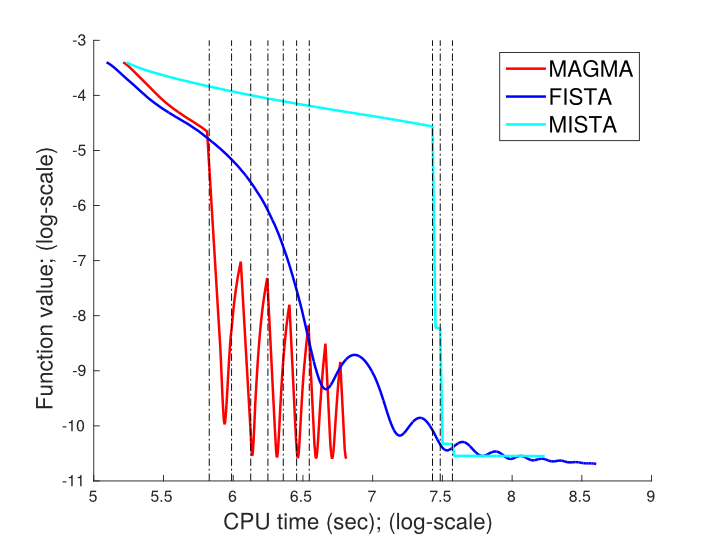
We compared our algorithm (MAGMA) to one of the most widely used algorithms - FISTA, and the only other multi-level algorithm that can handle composite structures - MISTA, on an face recognition problem. The aim of face recognition is given a database of facial images and another incoming image, recognize the owner of the incoming image from the database. We applied the algorithms on several large databases (with up to 8825 images in it) of images captured in controlled and in uncontrolled conditions. The fine model has tens of thousands of variables. We then used lower resolution models and MAGMA to speed up the computations.In the left figure below we compare the three algorithms in terms of function value progress on a database of 8,825 images. The results shown are for a single image and database. MAGMA and MISTA perform more expensive iterations than FISTA, so to be fair we compare the algorithms in terms of CPU time. MAGMA clearly outperforms the other algorithms. In the right figure below we show the relative CPU times until convergence of MAGMA and MISTA compared to FISTA for several experiments run on the same database with 20 random incoming images and 4 random initializaions for each image. MAGMA is in average five times faster than both FISTA and MISTA.
The code and images used in the experiments above are available
here.