Importance Sampling in Stochastic Programming with MCMC
Stochastic programming models are large-scale optimization problems that are used to facilitate decision-making under uncertainty. Optimization algorithms for such problems need to evaluate the expected future costs of current decisions, often referred to as the recourse function. In practice, this calculation is computationally expensive. The same issue arises in dynamic programming where the cost-to-go function or value function needs to be estimated.
If the recourse function is not evaluated accrutely then algorithms such as Stochastic Dual Dynamic Programming generate invalid supporting hyperplanes (cuts). This is explained in our paper in more detail and illustrated in the picture below.
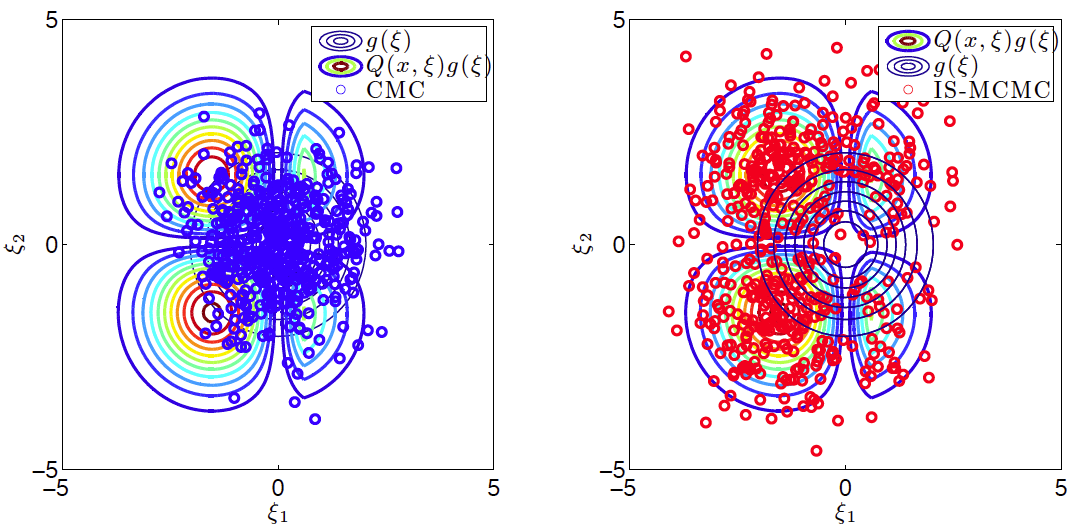
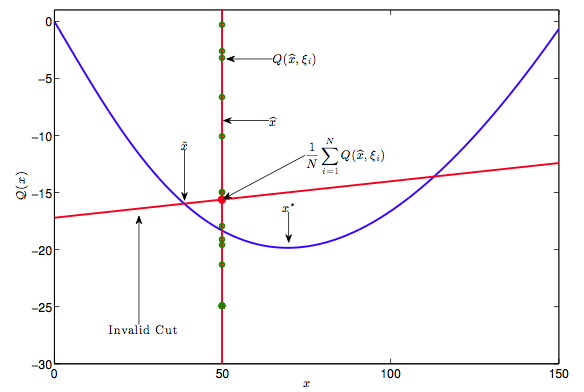The solution is simple, just sample more! The problem is that sampling is expensive as for every sample an optimisation problem needs to be solved. The solution we proposed is to use MCMC to discover the ``important" areas to sample. This means that we waste some samples in order to discover the most promosing areas. In the end we have less samples but of high quality. This is illustrated in the picture below. In the left are the samples generated with crude Monte Carlo and on the right the samples generated with our algorithm. The contours show the relative importance of the samples.
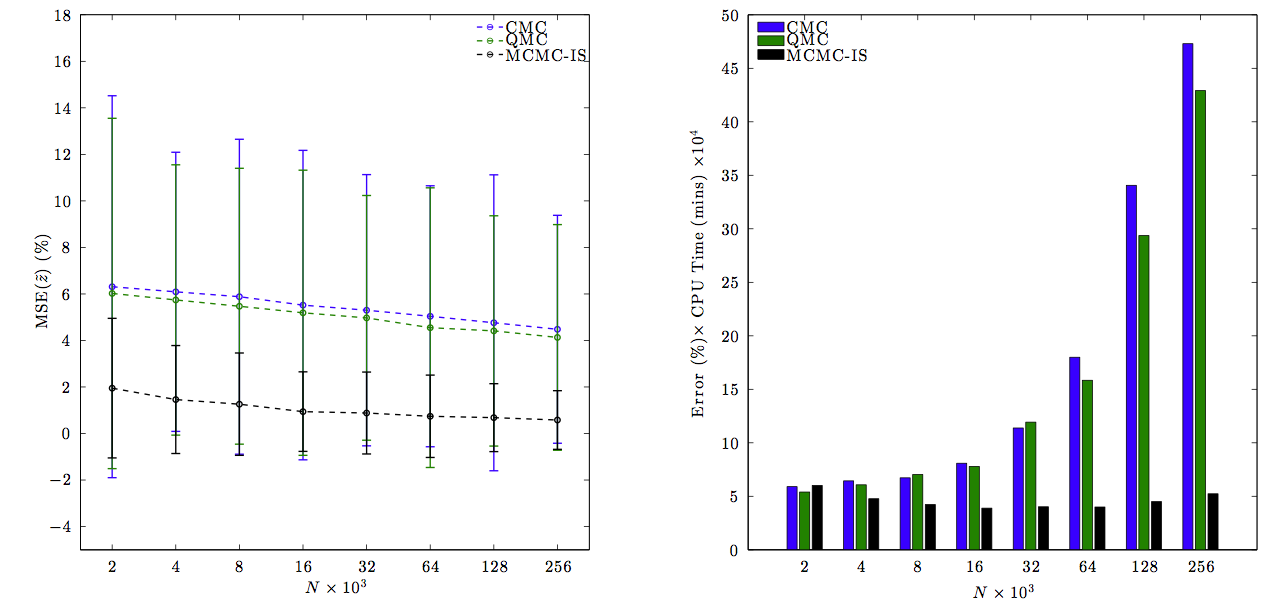
We tested this idea on several test problems and the details are in the paper. We summarise some of the results below. The basic outcome is that we can acheive less error and higher accuracy than Crude Monte Carlo (CMC) and Quasi Monte Carlo (QMC) methods (see picture on the left below). Of course there is a time penalty for imporving the quality of the samples but the error per unit of CPU time is much less for our method than other sampling methods (see picture on the right below).
Reference
@unpublished{parpasustunwebstertran2013,Title = {Importance Sampling in Stochastic Programming: A Markov Chain Monte Carlo Approach},
Author = {P. Parpas and B. Ustun and M. Webster and Q. Tran},
Note = {INFORMS Journal on Computing. },
Year = {forthcoming}}