The Mandelbrot Set

Introduction

The interest in fractal geometry initially arose from the observation of self-similar patterns in nature. One of the first mathematicians who referenced the idea of self-similarity was Leibniz in the 17^th century. However, the concept of fractals as we understand them now was not developed until two centuries later. We could highlight for instance the work of Georg Cantor on the Cantor set or the contributions of Helge von Koch, who geometrically exemplified the phenomenon with the so called Koch snowflake. The field of fractal geometry kept evolving, with more abstract approaches such as extending the idea to multiple dimensions.^[1]

These advances eventually led us to the mathematical object at issue: The Mandelbrot Set, discovered in 1979 by the mathematician Benoit Mandelbrot. Author of the famous paper How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension^[2], he worked as a researcher at IBM and it was thanks to the powerful computers he had at his disposition that he could plot this emblem of mathematics.^[3][4]

The Mandelbrot Set

The Mandelbrot set^[5] is related to the behaviour of following complex one dimensional map over infinite iterations: \begin{equation} z_{k+1} = z_{k}^2 + c \end{equation} Where $z, c \in \mathbb{C}$ and $z_{0} = 0$. We say that the Mandelbrot Set is the set of points $c \in \mathbb{C}$ that when plugged in Eq. (1), converge as $k \rightarrow \infty$.

Figure 1 represents these $c$-values plotted in a complex plane bounded within $-1.2 \leq Im(c) \leq 1.2$ and $-2.1 \leq Re(c) \leq 0.7$. It is also important to remark what colours mean in this representation. The main light blue area represents the actual points that belong to the set, whereas the gradient of colours from blue to black is given by the number of iterations necessary to reach the escape condition.^[6]

Proof. We intend to prove that $|z| > 2 \implies |z^2 + c| > |z|$ (i.e. diverges). First suppose that $|z| > 2$ which, invoking the function definition can be rewritten as $|z^2 + c| > 2$. From the triangle inequality^[7] we also know that $|z^2 + c| + |c| \geq |z^2|$. Therefore: \begin{align*} |z^2 + c| &\geq |z^2| - |c| && \text{By the triangle inequality.}\\ |z^2 + c| &> 2|z| - |c| && \text{By the assumption that $|z| > 2$.} \tag{*}\\ \end{align*} Now we need to show that $|z| \geq |c|$ which can be obtained by considering the first iterations: \begin{align*} |z_{1}| &= |c|\\ |z_{2}| &= |c^2 + c| = |c||c + 1| > |c|\\ &\vdots \\ |z_{n}| &> |c|\\ \end{align*} At this point it can easily be deduced that $2|z| - |c| \geq |c|$ from the last result because $|z| \geq |c| \implies |z| - |c| \geq 0 \implies 2|z| - |c| \geq |z| \geq |c|$. This statement combined with (*) leads us to $|z^2 + c| > |z|$ q.e.d.^[8][9]

Saying that the Mandelbrot set is restricted to $|z_{k}| \leq 2$ is equivalent to saying that all the elements are contained in the disk of radius 2 around the origin, which implies it's bounded. Furthermore, from the lemma just proven, it is obvious that all the limit points^[15][16] lie in the set. So we can conclude that the Mandelbrot set is a compact set.

Finally, we'll demonstrate the relationship between the sequence of real points $c_{k} = a_{k} + 0i$ in the Mandelbrot set and the period-doubling cascade $a_{k}$ of the logistic map.

The relationship between logistic maps and the Mandelbrot set follows from a redefinition of the variables. We need to allow $x,r \in \mathbb{C}$ and perform the following variable changes: \begin{align*} z_{n} &= r(x_{n} - \frac{1}{2})\\ c &= \frac{1-(r-1)^2}{4} \end{align*} Now, using simple arithmetic we can rewrite the equation: \begin{align*} x_{n+1} &= rx_{n}(1 - x_{n})\\ x_{n+1} &= r(\frac{1}{4} - (x_{n} - \frac{1}{2})^2)\\ &\vdots \\ z_{n+1} &= z_{n}^2 + c \end{align*} At this point, we can intuitively deduce that both are representations of the same phenomenon. Let's consider the following graph, which we'll use to deepen our understanding about this relationship.

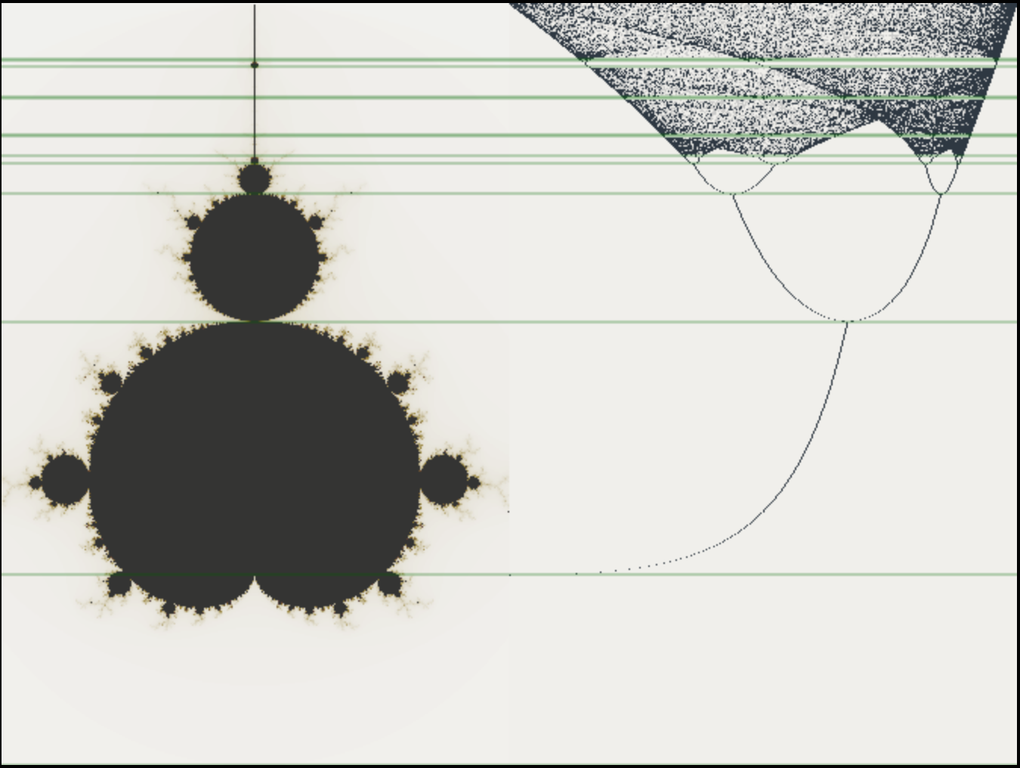
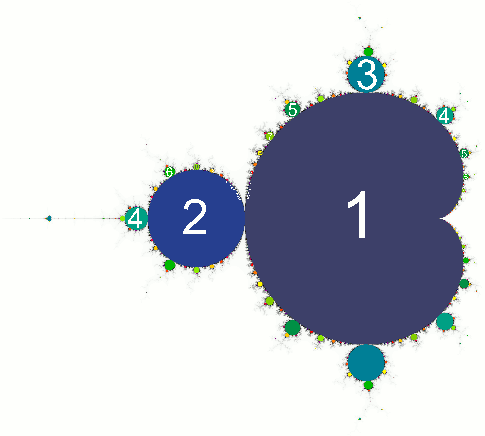
It is important to mention that each graph represents in Figure 1 a different face of the quadratic map. While the Mandelbrot set represents all the points that converge, the logistic bifurcation map gives the actual values of the period-doubling points for every given r. Even though this information is not directly provided by the Mandelbrot set, each cardioid is actually associated to a certain periodicity (as we can see in Figure 3). This fact together with the previous connection found between $r$ and $c$ clarify why every new cardioid found moving along the real axis in the Mandelbrot set represents a period-doubling point.^[18][19][20]