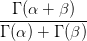Beta Distribution and Dirichlet Distribution

Wenjia Bai

October 30, 2012

  1. Title: http://en.wikipedia.org/wiki/Beta_distribution
  2. Title: http://mathworld.wolfram.com/BetaDistribution.html
  3. Title: http://en.wikipedia.org/wiki/Dirichlet_distribution

1 Beta Distribution

1.1 Definition

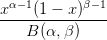
Beta distribution is a type of statistical distribution, which has two free parameters. It is used as a prior distribution in Bayesian inference, due to the fact that it is the conjugate prior distribution for the binomial distribution, which means that the posterior distribution and the prior distribution are in the same family.

The probability distribution function (pdf) of the beta distribution is defined as,

f(x; α,β) = 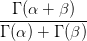Γ (α + β ) ------------ Γ (α ) + Γ (β)xα−1(1 − x)β−1
= xα−-1(1 −-x-)β−1 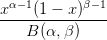B (α, β) (1)
where α > 0, β > 0, x ∈ [0, 1] and Γ(⋅) denotes the gamma function.

1.2 Application

Considering the classical Bernoulli problem (repeated coin flipping), after n trials, there are s successes (heads) and f failures (tails). Let a random variable x denote the success probability of each trial. The likelihood for parameters s and f given x = p is is the following binomial distribution,

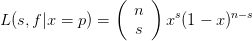( n ) L(s,f |x = p ) = xs (1 − x )n− s s
(2)

If belief about prior probability information is reasonably well approximated by a beta distribution,

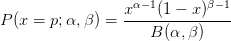x α−1(1 − x)β−1 P (x = p;α, β) = --------------- B (α,β)
(3)

According to Bayes’s theorem, the posterior probability is given by the product of the likelihood function and the prior probability normalised by the integral as follows,

P(x = p|s,f) = 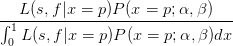L(s,f|x = p )P (x = p;α, β) ∫-1----------------------------- 0 L(s,f |x = p)P(x = p; α,β)dx
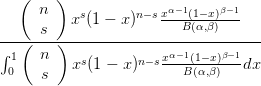= ( n ) α−1 β−1 xs(1 − x)n−sx--B(1(−αx,β))--- ---(-s--)--------------------------- ∫ 1 n s n−sxα−1(1−-x)β−1 0 s x (1 − x) B(α,β) dx
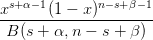= s+α− 1 n− s+ β−1 x------(1-−-x-)------- B (s + α, n − s + β) (4)
The posterior probability function is also a beta distribution (conjugate). It is convenient to compute. This is the main reason why we approximate the prior using a beta distribution.

PIC

Figure 1: Bayes’s prior probability, Beta(1,1).

PIC

Figure 2: Jeffrey’s prior probability, Beta(1/2,1/2).

PIC

Figure 3: Haldane’s prior probability, Beta(0,0).

For the Bayes’s prior probability (Beta(1,1), Figure 1), the posterior probability is,

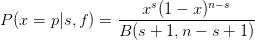s n−s P(x = p|s,f ) = ---x-(1-−-x)------- B (s + 1,n − s + 1 )

with mean = 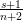sn++12- and mode = sn.

For the Jeffrey’s prior probability (Beta(1/2,1/2), Figure 2), the posterior probability is,

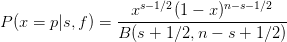xs− 1∕2(1 − x)n−s−1∕2 P (x = p|s,f ) = ------------------------ B(s + 1∕2,n − s + 1 ∕2)

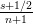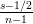with mean = s+1∕2 -n+1- and mode = s−1∕2 -n−1-.

For the Haldane’s prior probability (Beta(0,0), Figure 3), the posterior probability is,

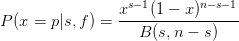s−1 n−s−1 P (x = p|s, f) = x---(1-−-x)------ B (s,n − s)

with mean = sn and mode = sn−−12-.

2 Dirichlet Distribution

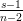The Dirichlet distribution is a family of continuous multivariate probability distributions parameterised by a vector α of positive reals. It is the multivariate generalisation of the beta distribution. It is often used as the prior distribution in Bayesian inference and it is the conjugate prior of the categorical distribution and multinomial distribution.

The pdf of the Dirichlet distribution is defined as,

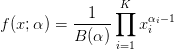1 ∏K f(x; α) = ----- xαii−1 B (α) i=1
(5)

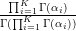where α = (α1,α2,⋅⋅⋅,αK) denotes the concentration parameters (αi > 0), K ≥ 2 denotes the number of categories, B(α) = ∏K --∏i=K1Γ (αi) Γ ( i=1Γ (αi)), and the support x = (x1,x2,⋅⋅⋅,xK) follows xi ∈ [0, 1] and ∑ ixi = 1. The support is in fact a simplex.