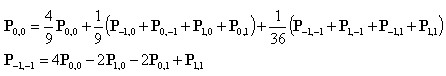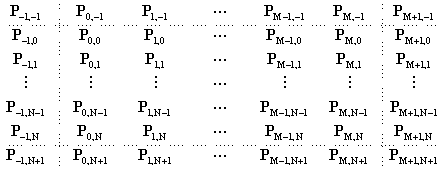
We can create a B-Spline surface using a similar method to the Bézier surface. For B-Spline curves, we used two phantom knots to clamp the ends of the curve. For a surface, we will have phantom knots all around the eal knots as shown below for an M+1 by N+1 knot surface.

There are two extra rows and two extra columns of knots in parametric space surrounding the real knots. Where we place these knots determines the shape of the surface at the edges. The method described here gives similar results to the method used for Bézier surfaces; that is, the edges of the surface form a B-Spline curve of the edge knots. This means some of the boundary conditions are
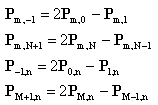
for 0 <= m <= M and 0 <= n <= N. These conditions are essentially the same as the two-dimensional case. They mean the weighting of a sample taken at the boundary m=0 is dependent only on knots along the m=0 boundary (the phantom knots at m=-1 balance out the real knots at m=1). The remaining boundary conditions make the surface corners and the corner knots coincide. The co-ordinate of the corner as set by P0,0 (and hence the parametric knot at {-1,-1}) is