Parallel Composition "||"
( P || Q)
expresses the parallel composition of the processes P and Q. It constructs an LTS which allows all the possible interleavings of the actions of the two processes. Actions, which occur in the alphabets of both P and Q, constrain the interleaving since these actions must be carried out by both of the processes at the same time. These shared actions synchronise the execution of the two processes. If the processes contain no shared actions then the composite state machine will describe all interleavings. In the following example, x is an action shared by the processes A and B.A = (a -> x -> A). B = (b -> x -> B). ||SYS = (A || B).
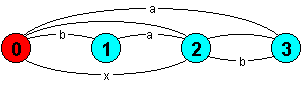
The diagram depicts the LTS for the composite process SYS. It can be easily seen that, in this simple example, the two possible execution traces are < a,b,x> and <b,a,x>. That is the actions a and b can occur in any order. Composite process declarations are distinguished from primitive process declarations by prefixing with the symbol ||. Primitive processes may not contain the parallel composition operator and composite processes may not use action prefix, choice or recursion. This separation is partly to ensure that FSP can only generate finite systems. The parallel composition operator is n-ary. The following example, with three processes, is a system describing the behaviour of a garage shared between two cars.
CAR(I=1) = (car[I].outside -> car[I].enter ->
car[I].ingarage -> car[I].exit -> CAR).
GARAGE(N=2) = (car[x:1..N].enter -> car[x].exit -> GARAGE).
||SHARE = (CAR(1) || CAR(2) || GARAGE).
Note that an action label may consist of more than one identifier (optionally indexed) joined by ".". Processes referred to in composite process definitions may be either primitive or composite. So, for example, SHARE can be constructed in two stages:
||CARS = (CAR(1) || CAR(2)). ||SHARE = (CARS || GARAGE).
The garage system could be more elegantly expressed using process labelling as shown below:
CAR = (outside -> enter -> ingarage -> exit -> CAR). GARAGE(N=2) = (car[x:1..N].enter -> car[x].exit -> GARAGE). ||SHARE = (car[1]:CAR || car[2]:CAR || GARAGE).
The construction car[1]:CAR prefixes all action labels within CAR with the label car[1]. Finally, we can generalise the description such that it describes a systems with N cars sharing the garage:
||SHARE(N=3) = (car[1..N]:CAR || GARAGE(N)).
The || operator is commutative (P||Q º Q||P).