
Unfortunately, it is necessary for you to learn some math in the network security course. If you had a look at the course notes, you know what I mean. Security has borrowed many tools from mathematics (see the list below for some examples) and in some sense, many theories in security can be seen as the natural progressions of mathematics. This is particularly true of cryptography.
Group theory, Finite Field theory, Number Theory, Algebraic geometry: cryptography
Lattice Theory: access control, cryptography, secure information flow
Probability theory, Statistics: risk management, intrusion detection, privacy protection
Game theory: Security model
Logic: security policies, verification and analysis of security protocols
Mathematics also allows people to formally define and rigorously prove security. This is another point why mathematics is so important in security. For example, if you designed a new cipher, how can you convince me that your cipher is secure?
Answer 1: “I cannot break it, so it must be secure”. No, anyone can create a cipher that he himself cannot break. However, the question is whether there is anyone more clever who can break it. Click here to see some examples of ciphers which have been broken.
Answer 2: “My cipher uses xxx-bit keys, so it is secure”. No, key size does not guarantee anything. A trivial counter example is a cipher which has 1024-bit key size and just encrypts the plaintext by breaking the plaintext into several 1024-bit blocks and xoring the blocks with the key. This cipher has a large key size but is easy to break.
Answer 3: “No one can recover the plaintext given the corresponding ciphertext generated from my cipher”. No. Imagine I designed a cipher which actually leaves half of the plaintext unencrypted. Obviously no one would use it in any application. However it would be "secure" according to the definition as long as I can make the other half of the plaintext hard to recover.
Answer 4: “No one can recover any part of the plaintext given the corresponding ciphertext generated from my cipher”. It sounds better, however is still not good enough. For example, some ciphers are deterministic which means they always produce the same ciphertext for a given plaintext and key. You may not be able to recover the plaintext, however you know two ciphertexts correspond to the same plaintext if they are identical. The ciphertexts generated from these ciphers, although revealing no direct information, reveal some indirect information about the plaintexts.
Answer 5: “The ciphertext reveals no useful information about the corresponding plaintext”. I think that is the farthest you can go without mathematics. However, what exactly does "reveal no useful information" mean? Can you measure the information leaked by the ciphertext? This definition is not wrong, but imprecise.
Here is an example how to mathematically construct and cipher and how to define and prove security using formal math language.
In 1917, Gilbert Vernam invented a cipher for use on telex machines. The idea is quite simple. At the sender side, each transmitted 5-bit Baudot code was mixed with a random 5-bit code on a paper tape (see the graph below). At the receiver side, a copy of the tape used in encryption is used to decrypt the ciphertext. The mathematical operation used in encryption and decryption is XOR (exclusive OR). The key has the same length as the message and must be used only once.
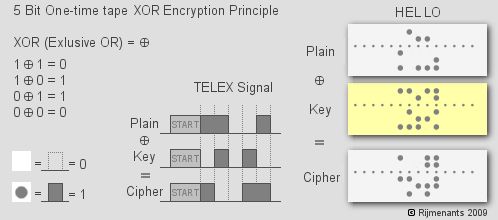
In his paper, Vernam claimed : If the key used with this type of cipher is made very long, so that it never repeats and if any portion of this key is never used for more than one message, the operation of "breaking" the cipher becomes very much more difficult. If, now, instead of using English words or sentences, we employ a key composed of letters selected absolutely at random, a cipher system is produced which is absolutely unbreakable. This claim, however had been left unproved until 25 years later Claude Shannon introduced the concept of perfect secrecy and demonstrated that the Vernam cipher archives this level of security.
So what is perfect secrecy? A cipher is perfectly secret if for every message m and every ciphertext c we have:
How to read this equation? M is a random
variable representing all possible plaintexts and C
is a random varaible representing all possible ciphertexts.
Is the Vernam cipher perfectly secret? Before giving the proof, let us have a look at a simple case so you will have an intuitive conviction. Consider now you have only one bit to encrypt. So the plaintext M can be either 0 or 1. Let the probability of M=0 be p, then the probability of M=1 is 1-p. Since the plaintext is only one bit, in Vernam cipher, you generate a one-bit key randomly. The relation ship between the plaintexts, keys, ciphertext and the probabilities can be summarised in the following table:
| K=0 (0.5) | K=1 (0.5) | |
| M=0 (p) | C=0 (p1 = 0.5p) | C=1 (p2 = 0.5p) |
| M=1 (1-p) | C=1 (p3 = 0.5(1-p)) | C=0 (p4 = 0.5(1-p)) |
If the ciphertext you've got is 0, then the plaintext can be 0 in the case that the key is 0, or the plaintext can be 1 in the case that the key is 1. Similarly, if the ciphertext you've got is 1, then the plaintext can be 0 in the case the key is 1, or the plaintext can be 1 in the case that the key is 0. Then the following four probabilities can be calculated:
Pr[M=0|C=0] = p1/(p1+p4) = 0.5p/(0.5p+0.5-0.5p) = p = Pr[M=0]
Pr[M=1|C=0] = p4/(p1+p4) = 0.5(1-p)/(0.5p+0.5-0.5p) = 1-p = Pr[M=1]
Pr[M=0|C=1] = p2/(p2+p3) = 0.5p/(0.5p+0.5-0.5p) = p = Pr[M=0]
Pr[M=1|C=1] = p3/(p2+p3) = 0.5(1-p)/(0.5p+0.5-0.5p) = 1-p = Pr[M=1]
So in one-bit case, the Vernam cipher indeed satisfies the definition of perfect secrecy. The general proof for arbitrary length Vernam cipher follows the same intuition. If you are interested, you can find it here.
This page was translated into Estonian by Weronika Pawlak at https://www.piecesauto-pro.fr/blog/2017/11/07/matemaatika-ja-turvalisus/.