332 Advanced Computer Architecture

Exercise 7 (Assessed): the sparse matrix-vector Challenge

This is the second of two assessed coursework exercises, both based on sparse matrix-vector multiply within the Markov chain solver ``csteady''.

You may work in groups of two or three if you wish, but your report must include an explicit statement of who did what.

Deadline: Thursday 11th March. Submit your work at the DoC Student General Office in a suitable labelled folder.

Background (as for exercise 4)

A sparse matrix is one with a large proportion of zero elements. Many important algorithms involve multiplying a sparse matrix by a vector, 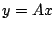$y = Ax$. This key computational ``kernel'' is the focus of the main laboratory project for this course.

Applications include:

Dense (that is not sparse) matrix-vector multiplication looks like this: 
   double A[A_rows][A_cols];
   double x[A_rows], y[A_rows];

   for ( i=0; i<A_rows; i++ ) {
      sum = 0.0;
      for ( k=1; k<=A_cols; k++ ) 
        sum += A[i][k]*x[k];
      y[i] = sum;
   }
To make this sparse we need a storage scheme. A popular choice is ``compressed row'': 
    struct MatrixElement {
      long col;
      double val;
    };
    /* no of non-zeroes in each row */
    int SA_entries[A_rows]; 

    /* array of pointers to list of non-zeroes in each row */
    MatrixElement** SA = (struct MatrixElement**)
                         malloc(sizeof(struct MatrixElement)*A_rows);
    
    /* When SA_entries is known we can allocate just enough memory for data */
    for(i=0; i<A_rows; i++) {
      SA[i] = (struct MatrixElement*)
              malloc(sizeof(struct MatrixElement)*A_entries[i]);
    }
The idea here is that for each row, we keep an array of the non-zero matrix elements, pointed to by SA[i]. For each element SA[i][j] we need its value, and its column number. So, if A[i][j] is the nth non-zero in row i, its value will be stored at SA[i][n].val, and SA[i][n].col will be j.

Now the matrix-vector multiply can be written as: 

    for(i=0; i<A_rows; i++) {
      sum = 0;
      for(j=0; j<SA_entries[i]; j++) {
        sum += ((SA[i][j]).val)*x[(SA[i][j]).col]; 
      }
      y[i] = sum;
    }

Compiling and running Csteady (slightly different from Exs4&5)

Copy the source code directory tree to your own directory: 
cd 
cp -r /homes/phjk/ToyPrograms/C/smv-V3 ./
Now run some setup scripts: 
cd smv-V3
source SOURCEME.csh
./scripts/MakeMatrices.sh 1 2 3 4
This creates a directory /tmp/USERNAME/spmv/ and builds some sample matrices there for problem size 1-4 (the matrix files are extremely large). You should compile the application using the following commands: 
pushd solver/csteady/
make
Now you can run the program: 
./csteady inputs/courier4/
This reads input from the directory for problem size 4, and writes its output to a file called ``STEADY'' in the same directory. This is problem size 4 - intermediate (133MBytes, ca.10 seconds). Problem size 5 (467MB) takes roughly 30-60 seconds.

All-out performance

Basically, your job is to figure out how to run csteady fast as you possibly can, and to write a brief report explaining how you did it.

Rules

  1. You can choose any hardware platform you wish. You are encouraged to find interesting and diverse machines to experiment with. The goal is high performance on your chosen platform so it is OK to choose an interesting machine even if it's not the fastest available. On linux type ``cat /proc/cpuinfo''. Try the Apple G5s.

  2. Make sure the machine is quiescent before doing timing experiments. Always repeat experiments for statistical significance.

  3. Choose a problem size which suits the performance of the machine you choose - the runtime must be large enough for an improvements to be evident. In practice, this program is used for much larger problems than we are able to study here.

  4. The numerical results reported by the application need not be absolutely identical, but number of iterations must be the same.1

  5. You can achieve full marks even if you do not achieve the maximum performance.

  6. Marks are awarded for

  7. You should produce a compact report in the style of an academic paper for presentation at an international conference such as Supercomputing (www.sc2000.org). The report must not be more than 7 pages in length.

Hints, tools and techniques

Memory: if your machine doesn't have enough memory the matrix generation phase can take a long time, due to thrashing. Use a smaller problem size.

Performance analysis tools:

You may find it useful to find out about:

Compilers

You could investigate the potential benefits of more sophisticated compiler techniques:

Source code modifications

Note that the matrix-vector multiply loop can be executed in any order - although this does lead to slightly different answers, as long as the solver converges it should be OK.

How to finish

The main criterion for assessment is this: you should have a reasonably sensible hypothesis for how to improve performance, and you should evaluate your hypothesis in a systematic way, using experiments together, if possible, with analysis.

What to hand in

Hand in a concise report which Please do not write more than seven pages.


Paul Kelly, Imperial College, 2004

Footnotes

... same.1
The real test is whether, when you run ``scripts/analyse-results.sh'', the metrics are the same. However to use this you need to modify ``./scripts/MakeMatrices'' so it doesn't delete the STATE matrix.
... machine)2
To use this, use a Windows machine and copy the smv-V3-cygwin version of the code (and data - you need cygwin to generate it yourself). See solver/csteady-msvc especially csteadyproj/csteadyproj.atp.
next_inactive up previous