I study situations in which multiple agents take decisions in complex environments and try to exploit the information they have about the system in order to realise their objectives.

I'm particularly interested in agents that can influence one another and how to engineer systems in which this social influence yields desirable outcomes.

I'm also interested in situations in which agents have very limited knowledge of the world around and need to take a good decision anyway.

Here are two examples of my research.

Engineering social interaction

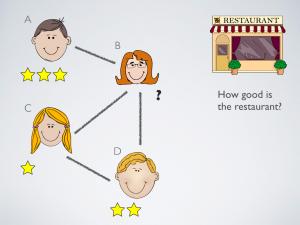
Imagine to be the owner of a new and still relatively unknown restaurant. The quality of food is not spectacular and the customers you have seen so far are only limited to a tiny number of friends of yours. Your account on Tripadvisor has received no review and your financial prospects look grim at best.

There is one easy solution to your problems: you ask your friends to write an enthusiastic review for you, possibly in exchange for a free meal. After this, Tripadvisor lists your restaurant as excellent and the number of customers, together with your profit, suddenly florishes.

Systems such as Tripadvisor, where a small proportion of customers writes reviews and influences a large number of potential customers, are not "bribery-proof": each restaurant owner is able to offer a compensation - monetary or not - in exchange for positive evaluation, having an impact on the whole set of potential customers.

Can we design a better system that, by constraining the way people can influence on another, can resist to malicious external agents? In other words, can we come up with bribery-proof rating systems?

I proposed, with Umberto Grandi, a "bribery-proof" rating system which you can find here.

Decision-making with incomplete information

You are playing the following position as Black and you have 10 seconds to move.

What would you do?

There are not many moves you can make, but each of them requires a deep calculation in order to be properly assessed. In time pressure we --- and the same goes for grandmasters and supercomputers --- make judgment calls. It might be that your first thought was to push the pawn to b2. This is the most "natural" move. After all, the pawn gets closer to the queening square b1, and after you queen the pawn you are going to have a decisive material advantage. True, but b2 happens to be the losing move. After b2 White has the surprising reply: Kf6! which forces you to queen the pawn. But then comes e7, and you are checkmated.

Now look at the following:

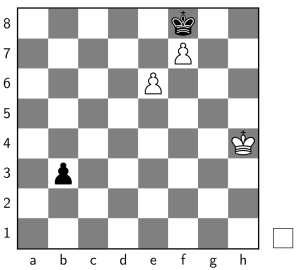
This position is very similar to the previous one, only White is to move and the king is on h4.

In this position, White is lost. But should he or she resign? My claim is that he or she should not resign, as long as he or she believes that the opponent will not see how to win, for instance if, after White moves the king back to g5, Black will blunder as above.

In general, what is a good way of making decisions in complicated games like Chess (or Go), where we know we cannot assess every position, but we also know that our opponents can't either?

I proposed a model for this type of decision problems which you can find here.