Symbolic Regression of A Quadratic Polynomial:
Genetic Programming is often used in the problem of symbolic regression where the goal is to automatically create a computer program whose output is equal to the values of the quadratic polynomial x2+x+1 in the range from −1 to +1.
Essentially there are 4 preparatory steps to the problem and this leads onto the executional steps of the actual running of Genetic Programming.
Preparatory Steps
The purpose of the first two preparatory steps is to specify the ingredients of the to-be-evolved program.- The terminal set (inputs to the to-be-evolved program) includes the independent variable, x. The terminal set also includes numerical constants. That is, the terminal set, T, is T = {X, A}, where A denotes constant numerical terminals in some reasonable range (say from − 5.0 to +5.0).
- The function set consists of the four ordinary arithmetic functions of addition, subtraction, multiplication, and the division function (%) which returns a value of 1 when division by 0 is attempted (including 0 divided by 0), but otherwise returns the quotient of its two arguments.. This choice is reasonable because mathematical expressions typically include these functions. Thus, the function set, F, for this problem is
F = {+, − , *, %}.
The third preparatory step involves constructing the fitness measure. - The purpose of the fitness measure is to specify what the human wants.
The high-level goal of this problem is to find a program whose output is equal to the
values of the quadratic polynomial x2+x+1. Therefore, the fitness assigned to a particular
individual in the population for this problem must reflect how closely the output of an
individual program comes to the target polynomial x2+x+1.
A smaller value of fitness (error) is better. A fitness (error) of zero would indicate a perfect score.
For most problems of symbolic regression or system identification, it is not practical or possible to analytically compute the value of the integral of the absolute error. Thus, in practice, the integral is numerically approximated using dozens or hundreds of different values of the independent variable x in the range between − 1.0 and +1.0. The population size in this small illustrative example will be just four. In actual practice, the population size for a run of genetic programming consists of thousands or millions of individuals. In actual practice, the crossover operation is commonly performed on about 90% of the individuals in the population; the reproduction operation is performed on about 8% of the population; the mutation operation is performed on about 1% of the population; and the architecture-altering operations are performed on perhaps 1% of the population. Because this illustrative example involves an abnormally small population of only four individuals, the crossover operation will be performed on two individuals and the mutation and reproduction operations will each be performed on one individual. - A reasonable termination criterion for this problem is that the run will continue from generation to generation until the fitness of some individual gets below 0.01.
Lastly the user has to specify the termination criterion.
Executional Steps
Once the human user has performed the preparatory steps, the executional steps shown in the flowchart of genetic programming are performed. Genetic programming starts by randomly creating a population of four(in our example) individual computer programs as shown in figure 1.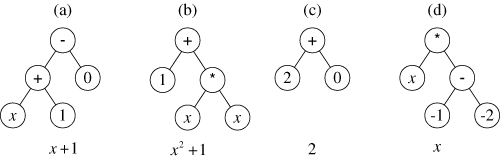
Figure 1 Initial population of four randomly created individuals of generation 0 ( © John Koza)
The first program is constructed by first choosing the subtraction function for the root (top point) of the program tree. The random construction process continued in a depth-first fashion (from left to right) and chose the addition function to be the first argument of the subtraction function, terminal x to be the first argument of the addition function and the constant terminal 1 as the second argument of the addition function Finally, the random construction process chose the constant terminal 0 as the second argument of the subtraction function (thereby terminating the entire construction process). The second program adds the constant terminal 1 to the result of multiplying x by x and is equivalent to x2+1. The third program (figure 1c) adds the constant terminal 2 to the constant terminal 0 and is equivalent to the constant value 2. The fourth program (figure 1d) is equivalent to x.

Figure 2 The fitness of each of the four randomly created individuals of generation 0 is equal to the area between two curves ( © John Koza)
As illustrated, the fitness is equal to the area between the parabola x2+x+1 and the curve representing the candidate individual. Figure 2 shows (as shaded areas) the integral of the absolute value of the errors between each of the four individuals in figure 1 and the target quadratic function x2+x+1. The integral of absolute error for the straight line x+1 (the first individual) is 0.67 . The integral of absolute error for the parabola x2+1 (the second individulis 1.0 . The integral of the absolute errors for the remaining two individuals are 1.67 and 2.67, respectively. Although the best-of-generation individual from generation 0 is not even a quadratic function, it is selected as the best candidate that happened to emerge from the blind random search of generation 0.
After the fitness of each individual in the population is ascertained, genetic programming then probabilistically selects relatively more fit programs from the population. The genetic operations (reproduction, mutation and crossover) are now applied to the selected individuals to create offspring programs.
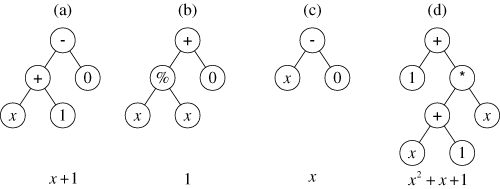
Figure 3 Population of generation 1 (after one reproduction, one mutation, and one two-offspring crossover operation) ( © John Koza)
In summary, genetic programming has, in this example, automatically created a computer program whose output is equal to the values of the quadratic polynomial x2+x+1 in the range from −1 to +1.
Back to EA In Action.