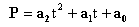
Parametric equations can be used to generate curves that are more general than explicit equations of the form y=f(x). A quadratic parametric spline may be written as
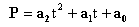
where P is a point on the curve, a0, a1 and a2 are three vectors defining the curve and t is the parameter. The curve passes through three points labelled P0, P1 and P2. By convention the curve starts from point P0 with parameter value t=0, goes through point P1 when t=t1 (0<t1<1) and finishes at P2 when t=1. Using these conventions we can solve for the three a vectors as follows:
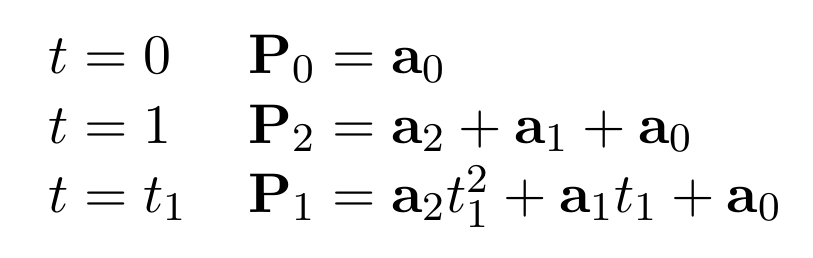
and rearranging these equations we get:
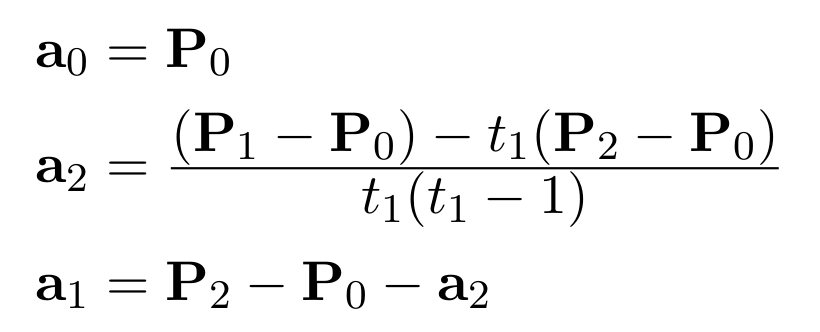
We can now apply this to any set of three points, as shown in the diagram below. It is easy to see the much higher degree of flexibility achieved through the use of parametric equations, and we will see this exploited with more advanced methods later on.
Figure 3.1 - Parametric Curve (interactive)
Although this method of creating curves is easy to use, it is not immediately clear how these shapes come about. The curve is actually a combination of two quadratic curves, one is y=f(t) and one is x=f(t). By varying t between 0 and 1, x and y will both vary and create the curve. This is shown below; create a curve and animate it to see how the three curves relate.
Figure 3.2 - Detail of Parametric Curve (interactive)