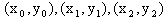 are three points on the
curve. The solution of these equations is
are three points on the
curve. The solution of these equations is
The most basic definition of a curve in two dimensions is y=f(x). This definition can be used to draw some simple curves. Although virtually any function can be used, the speed consideration for our application usually resticts us to polynomial functions, that is those where f(x) consists of powers of x only.
As an example, consider the cubic polynomial
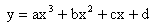
where a,b,c,d are constants. Together with a range for x, this defines a segment of curve. The shape of the curve is fairly flexible, but can't turn back on itself or be vertical. We could represent vertical curves using x=... instead, but the extra computational time involved in switching between the two methods inhibits the method's usefulness. The diagram below shows a cubic polynomial, with the four variables and the range of x available to change on the right hand side of the diagram.
Figure 2.1 - Cubic Curve (interactive)
It is clear the above curve is not very easy to manipulate. It would be much easier if we could move points on the curve on the diagram and see the curve change shape. Fortunately that's not too hard for a computer. I will only discuss the case for a quadratic curve here; the idea generalises to further degrees, but each extra degree adds another parameter and more complexity in the calculations. Given three points that are on a quadratic curve, there is only one solution, given by solving the three simultaneous equations
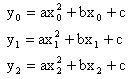
where  are three points on the
curve. The solution of these equations is
are three points on the
curve. The solution of these equations is
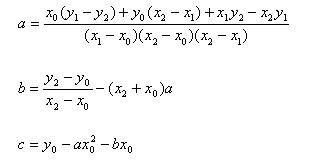
Therefore by using these equations we can draw a quadratic using any three points, so long as no two x or y values are identical. The diagram below illustrates this idea; it assumes the range of x is as wide as needed to accomodate the given points.
Figure 2.2 - Quadratic Curve (interactive)
This diagram illustrates the idea of designing a curve visually. It is much easier and more intuitive to describe a curve as a series of points through which it passes than using a list of parameters in an equation, as in the first example of this page. However, this method does have its limitations, which will be encountered later in this tutorial.