In this second part of the tutorial, we will be modelling a Map that associates unique keys with values (such as eg.
Map in Java) and show how Alloy can be used to explore dynamic behaviour.
The static aspects are easy to specify:
module examples/tutorial/Map
abstract sig Object {}
sig Key, Value extends Object {}
sig Map { values: Key -> Value }
As in Java,
abstract ensures that there cannot be any direct 'instances' of
Object. Similarly,
extends means that
Objects can either be
Keys or
Values, but not both.
values above is a
relation that represents the mapping of
Keys to
Values. This would be written in a schema in Object-Z as
values ⊆ K × V where K is the set of all Keys and V is the set of all Values.
We can visualize this model as before:
pred show() {}
run show for 2
The first instance produced by Alloy only consists of a
Key and a
Value but no
Map. We could browse through the various solutions until we find one that actually includes a
Map, however there is a better way.
As mentioned before, Alloy produces instances that satisfy the predicate passed to
run. We can add a constraint that specifies that there is at least one
Map:
pred show() { #Map > 0 }
run show for 2
We now get 2
Maps and one Value. To get exactly one
Map, we can either change the constraint to
#Map = 1
or we can modify the
run command as follows:
run show for 2 but exactly 1 Map
Next, let us check that the mapping of keys to values is unique. This can be done in Alloy via
assertions:
assert mappingIsUnique {
all m:Map, k:Key, v, v':Value |
k -> v in m.values and k -> v' in m.values implies v = v'
}
This says that if a
Map m maps a key
k to two values
v and
v' then they must be the same. Note how the relational product operator ("
->") in
k -> v is used to represent the tuple (k, v) and how
m.values is treated as a set of tuples
{(Key, Value)}. To check an assertion, we can use the command
check. As for
run, we have to specify the scope:
check mappingIsUnique for 2
If we execute this, Alloy searches all possible combinations of at most two objects of each signature for a counterexample that violates the assertion. Since it cannot find one, it tells us that the assertion may be valid. However, if we increase the scope to three, it produces the following:
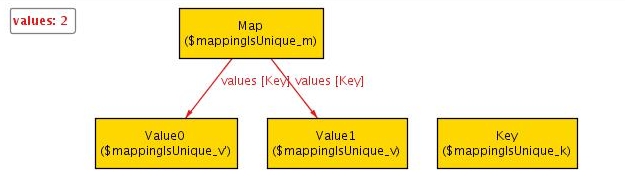
To make this even more obvious, we can ask Alloy to project over
Map using the Projection button:
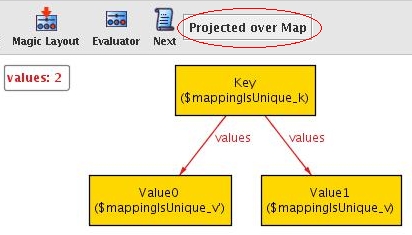
We see that a key refers to two values. To fix this, we use the
lone keyword that we have already seen:
sig Map { values: Key -> lone Value }
Now, the assertion holds even if we increase the scope to 15 (say). This produces a much larger coverage than any testcase ever could and gives us a high level of confidence that the assertion may be valid.
Finally, to make the instances of later steps less verbose, we include the constraint that all keys (and values) belong to some
Map:
fact {
all k:Key | some v:Value, m:Map | k -> v in m.values
all v:Value | some k:Key, m:Map | k -> v in m.values
}
Note that, unlike in the Queue example, it makes sense for a key/value to belong to more than one
Map. Also observe that the fact above is anonymous; Alloy does not require you to provide a name.
We have now developed the static aspects of the
Map. In the next section we will continue to develop the dynamics of our example.