- Introduction
- History
- First-Order Logic
- Clausal-Form Logic
- Prolog
- Logic Programming
- Summary
- FAQ
- Glossary
- References
Clausal-Form Logic (1)
Clausal form is a subset of first order logic. It is a normal form in which a sentence is defined by an universal prefix (a string of universal quantifiers) and a matrix (a quantifier-free conjunction of a clause). Here are a couple of examples of clauses:
a 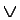 b
b 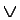 c
c
(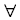 U)( healthy(U)
U)( healthy(U) 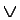 ¬eat(U, porridge) )
¬eat(U, porridge) )
The basic evaluation step of Prolog replaces a query call by the body of a program clause whose head it can match. This is the same as the application of an inference rule in logic, called resolution. A resolution inference step chooses two clauses having the property that one contains a disjunct X (a positive literal) and the other contains a disjunct ¬X (a negative literal), these disjuncts are known as complementary. A new clause (the resolvent) is constructed from the two initial clauses, using all the literals except the complementary ones. Here are a couple of examples:
- a
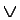 ¬b
¬b 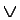 c
c - d
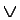 b
b
these "resolve" to produce - a
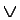 c
c 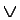 d
d
- (
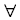 U)(healthy(U)
U)(healthy(U) 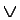 ¬eat(U, porridge))
¬eat(U, porridge)) - ¬healthy(sim)
these "resolve" to produce - ¬eat(sim, porridge)
Clauses can be classified by the number of positive and negative literals they contain.
| Clause Classification | Definition | Example |
| Definite | Exactly one positive literal, any number of negative literals | happy(sim) or ¬eating(sim, pie) |
| Positive unit | No negative literals | happy(sim) |
| Negative unit | Exactly one negative literal | ¬desirable(pop_music) |
| Unit | A positive or negative unit clause | |
| Negative | No positive literals, and any number of negative literals | ¬happy(sim) 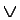 ¬eating(sim, snails) ¬eating(sim, snails) |
| Empty | No literals (denoted by  ) ) |
|
| Indefinite | At least two positive literals | happy(sim) 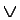 unhappy(sim) unhappy(sim) |
