Introduction
History
First-Order Logic
Clausal-Form Logic
Prolog
Logic Programming
- Higher-Order
- Constraint
- Concurrent
- Inductive
Summary
FAQ
Glossary
References

Higher-Order Logic Programming

Object orientated programming languages such as Java and C allow the programmer to create a class which is a set of objects. These classes contain access procedures which can be used to carry out operations on the instances of that class.

Object orientated programming is one type of high level programming language; it is popular because of the functionality and capability the language provides so there have been numerous attempts to develop similar functionality and capability into declarative programming languages.

Higher-Order Logic Programming languages such as Prolog and Twelf improve the notion of first order logic programming in two ways:

Dynamic assumptions are permitted and can be used during the execution.
Terms from the higher-order language are defined via 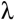abstraction.

When the code is executed, the result returned is not just True or False, it also produces a proof term as a certificate which can be checked independently.

The additional capabilities make higher-order logic programming an ideal tool for implementing and executing formal proof systems which are now in demand for further research in the AI field. The logic programming paradigm also provides the foundation for higher-order notations and principals. One of these is the use of 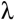LAMBDA calculus as representational devices and their unification forms are appropriate for implementing various structures. These modifications have improved the performance of the languages as well as enabling some important metaprogramming applications.

The disadvantages of the improvements of higher-order logic programming are non-trivial implementation problems. In particular, the machine representation and implementation of 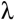LAMBDA terms and their suitability for proposed use. The appropriate encoding must provide adequate faculties for comparing the terms as well as reduction computation. Another important aspect to take into account is implementation of unification operations of the branching structures which sometimes causes a delay when solving unification problems.

To overcome the limitations, several features have been embedded into the traditional implementation of Prolog enabling it to support branching in unification as well as forwarding unification problems over their computation steps. The valid representation of 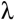LAMBDA terms has been developed using explicit encodings of the substructures.

The improved computation model handles higher-order unification as well as dynamic terms. One of the most recent developments in higher-order logic programming is Teyjus, which is an improved version of the 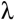LAMBDA Prolog language. It is used for preliminary assessment of efficiency.

The new capabilities of higher-order logic programming languages have improved existing theorem proving systems and expanded the horizons for further research in this field.