First-Order Logic (1)

< 1 2 3 >

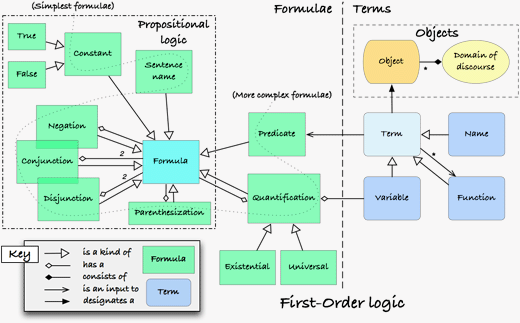
First order logic is an extension of propositional logic. It considers whether things are true or false in a partial view of the world, called a domain. Logic programming is based upon an extension of first-order logic. As first order logic is well understood and can be mathematically provable it can be used for representing all computational problems.

First order logic is made up of syntax and semantics. The syntax of first order logic is a formal language that is used to express concepts. The semantics of first order logic formulae tells us how to determine the truth value of any first order logic formula.

First order logic consists of an alphabet, a first order language, a set of axioms and a set of inference rules. The alphabet consists of seven classes of symbols:

• Variables - A sequence of alphanumeric characters that refer to objects in the domain.
  • e.g. u, v, w, x, y, z, foo.
• Constants - Represent objects in the domain.
  • e.g. a, b, c, Mary, Green.
• Function symbols - A relation among objects, of various arities greater than 0, that maps one object onto another.
  • e.g. f, g, h, fatherof(Mary), isBlue(sky).
• Predicate symbols - Maps one or more objects onto truth values.
  • e.g. p, q, r, greater(5,3), colour(Grass, Green).
• Connectives - Used to link together other members of the alphabet.
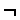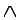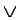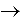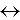  • e.g. , , , , .
• Quantifiers - Make an assertion about a formula applied over all objects in the domain.
  • e.g. 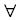(universal), 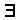(existential).
• Punctuation symbols - Used to make sentences more readable.
  • e.g. ')', '('

< 1 2 3 >