Imperial College Machine Learning - Neural Networks
There has been a lot of buzz surrounding neural networks in recent years with achievements made throughout various domains such as computer vision and natural language processing. The list of unprecedented successes such as DeepMind’s Gato model and OpenAI’s GPT-3 language model has been growing at rapidly. But what on Earth are neural networks? In these lecture notes and corresponding lectures we will explore, investigate and dissect some of the ideas behind neural networks. The learning is focused on an application basis, what is it, how does it work, when can we use it, how can we improve it with appreciation of the mathematical principles behind all this machinery. Throughout we will also be looking at some code examples from different libraries to see how theory is implemented in practice.
Inspired by / based on / referenced from: Artificial Intelligence: A Modern Approach (Peter Norvig and Stuart J. Russell), Deep Learning (Aaron C. Courville, Ian Goodfellow, and Yoshua Bengio), Course 6.036 Massachusetts Institute of Technology, Courses CS231 & CS224n Stanford University
Before we even begin, it is often a nice idea to establish the grounds we are going to explore. Let’s present most of the keywords we are going to encounter (not exhaustive but a good estimation), in no particular order:
- features, feature engineering, continuous / discrete data, one-hot encoding, architecture, weight, parameter, activation function, bias, neuron, perceptron, learning rate, layer, fully-connected / dense layer, feed-forward network, depth / width of network, deep learning, hidden layers, weight initialisation, linearity / non-linearity, piece-wise linear, loss function, regression, binary / multi-class / multi-label classification, cross-entropy, back-propagation, derivative, chain rule, vanishing gradients, gradient descent, objective function, local minimum, stochastic / mini-batch gradient descent, epoch, hyper-parameters, learning rate decay, training / validation / test data, over-fitting, under-fitting, early stopping, capacity, regularisation, weight decay, dropout, data augmentation, data normalisation, feature scaling.
If none of these keywords are familiar, or even if they are, don’t worry! As the course progresses and you read along, we will try to uncover the mysteries behind these keywords. Perhaps more importantly, the goals of this module from the learner’s perspective (you as the student) are, in other words the learning outcomes:
- Describe the module keywords.
- Implement and train a neural network to solve a machine learning task
- Summarise the steps of learning with neural networks
- Assess and improve the suitability of a neural network for a given task
Brief History
The ideas we will be looking at, neurons, neural networks etc. are not new by any reasonable measure although the mainstream hype would suggest otherwise. If you hear someone saying “back then neural networks didn’t exist”, take it with a pinch of salt and just double check if they were alive in the 1940s. Yes, that is roughly when the journey starts. In 1943, neurophysiologist Warren McCulloch and mathematician Walter Pitts put forth how neurons in the brain might work. Then in 1949, Donald Hebb suggested neural pathways of neurons that fire together strengthen over time which is often referred to as Hebbian Learning. These ideas led to Perceptron, an algorithm for binary classification which we will look at as the starting point of neural networks.
Pro Tip: If you are going to invent a new algorithm, model, paradigm make sure either your name / surname works well with it such as Dijkstra’s Shortest Path, Higgs Boson or find a really good catchy name like Perceptron.
Although these ideas were radical, there was little practical success, particularly their performance was limited compared to Support Vector Machines (SVM). The Perceptron could not learn anything that was not linearly separable for example. By the mid 1980s, several people came up with back-propagation that allowed to train more complex network architectures. These were slow and required many iterations / data to train for which computing resources were unavailable during that time. Hence the hype diminished once more.
So what happened in recent years? -> “Big data machine learning in the cloud.” More data and significantly more computing power meant that the ideas were revived from hibernation and started taking over the world. We collected vast amounts of data to train on and had the resources to do so compared to the 1990s where a few MB disk was considered luxury. These days datasets come in gigabytes and state-of-the-art models train on General Purpose Graphical Processing Units (GPGPU) or if you are Google you can use specialised silicon such as Tensor Processing Units (TPUs). Thus the hype started around 2012 when convolutional neural networks (a variant of what we are going to look at) started learning what a “dog” and “cat” is, published in this paper beating all other existing methods by a significant margin.
This is a very very crude history, I urge you to research on your own the various time periods of how things evolved. For example, what is the AI Winter some refer to?
The Task
What are we even trying to do? Good question, glad you asked because the rest of this module is somewhat useless if we don’t even briefly mention what the goal is. Fortunately, it is simple:
$$ y = f(x, \theta) $$We are given some data $x^{(1)}, x^{(2)}, x^{(3)}, \ldots$ which has a desired output $y^{(1)}, y^{(2)}, y^{(3)}, \ldots$ and our job is to learn the function $f$ that maps the input to the output by adjusting the parameters $\theta$. Nothing more, nothing less. The machine will not magically gain consciousness anytime soon.
Pro Tip: If it ever does feel like when you are training neural networks during this module - for example as part of the coursework - and it appears to be gaining consciousness -> unplug the Ethernet cable and disable any internet connection. Thank you.
This is the guiding principle behind many machine learning algorithms but it is worth clarifying here again. In the context of neural networks, machine learning refers to adjusting those $\theta$ parameters of the network such that they approximate a desired function.
Inputs - Outputs
So what are we giving a neural network and getting back? -> Numbers, just numbers, more likely just floating point numbers, more more likely just 32-bit floating point numbers. We must appreciate the fact that everything needs to be encoded as numbers to work with neural networks. Numerical input such as house prices is already in some numerical form which can be fed into a neural network. But what about text or speech? They get encoded into some number scheme, and it really depends on the problem how that is done. The inputs are also referred to as features of the entity, object etc. you are trying to learn something about. For example, the colour of the flower, the petal size and pattern are features of the flower that will help us classify which one it is. These are separate from learned features which refer to the hidden layers learning their own features.
To clarify, feature engineering refers to techniques applied to the input manually before they are fed into a neural network. These could be things like how many words that start with the capital letter and nouns in a sentence which might be extremely useful for predicting whether a given sentence is in German or not. However, this means the network doesn’t need to learn what a noun is or whether it starts with a capital letter, you are engineering those features yourself. On the other hand, learned features arise from hidden layers such as the networks learning lines, then corners using the learnt representations of lines, all the way up to ears and recognising a cat. More often than not we are interested in letting the network learn these and minimise the extent of manually engineering them.
Pro Tip: If someone tells you that their neural network learns to read twitter comments and predict their sentiment such as sad or happy, don’t be fooled that it actually learns human emotions. Their network is just learning a pattern between encoded versions of text and pre-defined numerical targets that map to pre-defined emotions.
Important announcement: Data is everything. Whether supervised or unsupervised, there is some data on which the neural networks / machine learning models act upon. So if your data suggests that smoking extends life, the neural network will not magically suggest a healthy life style, it will say start smoking instead. Let me make that point clear:
Data is everything
There are entire companies that are dedicated to outsourcing labelling data. What is a cat? What is a dog? Well someone needs to show the neural network what they are. Is this comment happy? Is this story sad? Is this fake news? Well, you need data, depending on the task, a lot of data to start training neural networks. Often the more complicated the problem, the more data you need. How much data? Machine translation from English to French has 15.8M sentence pairs, feel free to download it and explore although it will fill up your disk.
Pro Tip: If some stranger walks up to you and claims the problem with supervised learning is data so he or she is using or suggests using unsupervised learning, don’t be fooled. Unsupervised learning is when the data does not have labels like cat or dog but that doesn’t mean you don’t have or need large amounts of data. On the contrary, you might need more data because you are not supervising the network, it just learns some patterns in the data which might or might not (it could be garbage, most likely it will learn garbage if you just throw random data) be useful for something else.
Continuous
These inputs and outputs corresponding to numerical values that are innately a numeric value and are continuous. For example, heart rate, house price, stock price, distance, speed, angle are all continuous. Equally, we can ask a neural network to predict any of these values such as what the stock price would be in the future - good luck making money! It is important to also note that an image is also numerical in nature; each pixel is just a value indicating intensity or 3 values indicating red, green and blue components of that pixel. So one can argue these values are encoded already.
Source: Prof. Jonathan Bamber - Bristol University
Having numerical features doesn’t necessarily mean that one can just feed them into a neural network. There might be outliers, extremely large or extremely small values; perhaps the range of values might be skewed. We will look at some simple yet effective data techniques to overcome these. We are mentioning them here because as pointed out data is everything.
Discrete
This type of data is more common in classification. For example, text is discrete, you have individual characters or words. More importantly the outputs could be discrete: dog, cat, happy, sad. So how do we feed these into a neural network?
One way is to one-hot encode them. Given $N$ discrete values we construct a vector $v\in\mathcal{R}^N$ such that $i$th index is equal to one. For example, let’s have cities “London”, “Cambridge”, “Birmingham”, “Edinburgh” as our input for a potential address database and we want to include this as a feature to our neural network which might try to predict how tall on average people are (why not, we can try to learn other stuff but then again it depends on what and how much data we have). To include this feature we can one-hot encode them such that:
$$ \phi(London) = [1, 0, 0, 0]; \phi(Cambridge) = [0, 1, 0, 0]; \ldots $$Pro Tip: Even if you have a simple function such as setting a one in an otherwise lifeless vector, make sure you pick a nice Greek letter to represent it. And no I didn’t make this one up, $\phi$ is often used for feature transformation.
In fact this is such a common operation, most libraries include functions to do this. Often we have the index of the items in an array, so London will be 0 etc, for example using tf.one_hot:
# One-hot in Tensorflow:
tf.one_hot([0,1,2], 4) == [[1,0,0,0], [0,1,0,0], ...]
We can also convert continuous domains into discrete ones. For example instead of having numerical house prices, we can partition them into cheap, normal, expensive by some pre-defined values or convert temperature to high, medium, low depending on whether it is above 30 degrees, 20 degrees or not. Why would we do this at all? It depends on the application really, if it is a thermostat neural network (maybe not the best idea) you probably want the exact value of the temperature to control the boiler. But if we are learning about the plant life across various continents, having the exact temperature might not be necessary, whether it is hot or cold might suffice.
Pro Tip: You can roughly think of continuous data as measured and discrete as counted. We can measure the angle at which the robot moves its arm but we will have to count how many arms it has.
Neural Networks
Artificial neural networks are a class of machine learning models that are inspired by biological neurons and their connectionist nature. One way of looking at them is to achieve more complex models through connecting simpler components together. So what are the building blocks of neural networks? You guessed it: neurons. The architecture, i.e. the way in which neurons are organised and connected to each other give rise to different sub-classes of neural networks such as convolutional and recurrent. In this module we will be focusing on feed-forward neural networks (or sometimes also referred to as multi-layer perceptrons (MLP), we will analyse perceptrons soon).
Neuron
Representation of a single neuron
The building block of any neural network is a neuron. It is a unit that computes the following the function:
$ y = f(z) = f(\sum_i w_i x_i) = f(w^T x) $
which reads every input is multiplied by a corresponding weight and then summed to get $z$, the pre-activation value is then passed to the activation function $f$. The activation is often a non-linear function but we don’t necessarily need to specify one or we could set to be the identity function $x = f(x)$. Since we will soon deal with a lot of neurons, we often write these equations in vector form, so $w \in \mathcal{R}^{n \times 1}$ and $x \in \mathcal{R}^{n \times 1}$. In this case we are taking the dot-product of the two vectors and passing the result through the activation function, remember $w \cdot x = w^Tx$. As a heads up, when we have multiple neurons in a layer, the weights will become a matrix and activations a vector instead of a scalar. There will be just more numbers to handle and vectorised equations keep things organised although we can always write it in explicit summation form any time we want.
On the opposite end, we can simplify things to a single input and the equation becomes somewhat familiar:
$$ y = f(wx) $$This looks like the function of a line $y = wx+b$ but there is something we omitted: the bias. Often you’ll see $wx + b$ written as the equation, vector form or not. This is because we can absorb the bias into $w$ such that there is an extra input whose value is always 1. So $x' = [x, 1]; w = [w_1, w_0]$ and we get $y = w_1 x + w_0$ which is exactly the same as having an explicit bias value. Let’s briefly discuss what we have so far, there are some weights we are going to adjust depending on the input. The neuron roughly translates to: given some inputs, compute a linear combination of all of them, add (or subtract if negative) the bias and apply a function. The weights allow the neuron to create a custom, learnable combination of inputs while the bias acts like a learnable threshold.
Let’s compare this to a biological neuron:
Source: Wikimedia Commons
As you can see, there are many similarities between the biological one (which is amazing by the way, you should appreciate how evolution has come to the point of producing specialised cells that carry electrical signals using voltage differences caused by ions across a membrane and all of that leads to you being able to read these sequences of characters while constructing some meaning) and the artificial one. There are 2 ways to view neural networks and artificial neurons:
- A brain-inspired network that learns some functions. This view is common with the public who think we are building artificial brains of some sort and some day the machines are going to take over the world.
- An algebraic learnable transformation of inputs with respect to some outputs. This concept of mathematical transformations is the direction you should be getting more comfortable with. If you notice the equation, at its core has $w^Tx$ which is a linear transformation. As such we need to treat the entire topic to come with less magic but more mathematical grounding around linear algebra and calculus.
Pro Tip: Evolution had a lot of time to randomly explore solutions to problems we face, roughly 4 billion years ago life has started on Earth. In contrast the term personal computer was coined in 1975. So if there is a problem, you might need to get out of labs to find a solution.
Perceptron
We can actually do some things with a single neuron. Perceptron is an algorithm for supervised binary classification. Let’s break that down, we are supervising which means we have some labelled data $x^{(1)}, x^{(2)}, x^{(3)}, \ldots$ which has desired outputs $y^{(1)}, y^{(2)}, y^{(3)}, \ldots$ and we are trying to do binary classification, so there are 2 classes we want to predict, either class 0 or 1. Let’s take the activation function to be a threshold function:
$$ h_w(x) = f(w \cdot x) = 1 \text{ if } w \cdot x \ge 0 \text{ else } 0 $$Source: Wikimedia Commons
Then the perceptron learning rule to update the weights in order to learn this classification is:
$$ w_i \leftarrow w_i + \alpha(y - h_w(x)) \times x_i $$This is equation 18.7, chapter 18 from the textbook Artificial Intelligence: A Modern Approach. The $\alpha$ is the learning rate that allows us make smaller incremental changes rather than large jumps which can be unstable. Let’s analyse this equation to see what happens:
- if the desired output is equal to our prediction (perceptron output), $y = h_w(x)$ then the right hand side of the summation becomes 0 and the weights stay the same. Intuitively, don’t fix it if it isn’t broken.
- if $y = 1; h_w(x) = 0$ then the corresponding weight is increased when corresponding input is $x_i$ is positive and decreased when it’s negative. By doing so we want to make $w \cdot x$ bigger since the desired output is larger than our prediction.
- if $y = 0; h_w(x) = 1$ the opposite of the previous situation happens because we want to decrease the summation.
Source: Wikimedia Commons
This algorithm gives hint at how we can train neural networks: Adjust the weights in the direction of the desired output. For the single neuron case, this is analytically constructed, but what will happen when we have a lot of neurons chained together in layers? (The answer comes in later sections, I’m just building hype here.)
Before we dive into the large networks, what can we learn using perceptron? We can learn any linearly separable function using this algorithm. The proof of that is outside the scope of this module but let’s look at some examples:
Source: Medium - Solving XOR with a single Perceptron
On the left are two linearly separable functions OR, AND. You can see why they are linearly separable because a line can separate between the two desired classes 0 and 1. So the perceptron can learn the boolean functions AND, OR. More formally, linear separability is defined as, given two sets of points $X_1, X_2$ we have:
$$ w \cdot x + b > 0,\ x \in X_1\ \text{and}\ w \cdot x + b < 0,\ x \in X_2$$which reads that the two sets of points lie on either side of the line. But wait! What about XOR on the right? XOR is not linearly separable as there isn’t a line that can distinguish between the two outputs. Try drawing a line on the XOR chart such that one side of the line has white dots and the other side black dots, hint: you can’t.
In 1969, Marvin Minsky and Seymour Papert published a famous book titled Perceptrons and showed it was impossible for perceptron to learn the XOR function. What was missing? The problem was rooted in the linear nature of a single neuron with the threshold function. So we need a way to transform XOR into a linearly separable problem then we can solve it. What if that transformation was also learned? How about another layer of neurons that learn an intermediate transformation which then can be used to solve the XOR problem? You can see where this is going.
Pro Tip: These days you only hear about the success of neural networks and deep learning but not much about their failures. A failed result is as important and valuable as the successful one.
Layer
When we have multiple outputs or more importantly want to learn multiple intermediate transformations, features of the input we are given, we will need many neurons. This situation naturally leads us to organising them into a layer. A layer is a collection of neurons that share the same inputs but have different weights.
Single Neuron to Layer
We again have some inputs $x \in \mathcal{R}^{N \times 1}$ but this time (as aforementioned) the weights can be collected into a matrix $W \in \mathcal{R}^{N \times M}$ with bias $b \in \mathcal{R}^{M \times 1}$ producing $y \in \mathcal{R}^{M \times 1}$ outputs. The equation is just the vector form of a single neuron:
$$ y = f(W^Tx + b) $$Pro Tip: When you find yourself writing vector form equations and dealing with matrices, vectors, tensors, just checking the shapes match is a good starting point to make sure things work.
No surprise thus far. We just added more neurons together and each neuron produces it’s own output. Every neuron has the same computation but different weights. So although the computation is the same, the output will be different due to different weights. If you recall what a neuron did (you probably don’t so I’ll just say it again), it creates a learnable linear combination of its inputs passed through a non-linear activation function $f$, now we have $M$ many learnable combinations of the inputs. In essence, the layer now computes $M$ many different transformations of the input. This setup gives it the power to learn / transform / extract (these terms are used in different domains, usually what makes sense in the domain) for the given inputs / features. It is also important to note that the scalar activation function is applied element-wise to a vector: $f(x) = f([x_1, x_2, \ldots]) = [f(x_1), f(x_2), \ldots]$ where each element is passed through the function individually.
$$ \begin{aligned} z &= W^Tx + b \\ y &= f(z) \end{aligned} $$There is no requirement to apply the activation within the layer. We can separate the activation from the linear transformation. But why? There is nothing special about doing it in one go, in fact in most deep learning libraries they are separate or separable. You can perform the linear transformation in a layer and then later you can apply the activation. For example, if you want to multiply the output with another vector before the activation function, you would be able to do it which gives us that extra flexibility. You can think of activation as another computation that happens after $W^Tx$. This distinction is important when we start chaining these layers together to create a network.
# From https://github.com/keras-team/keras/blob/master/keras/layers/core.py
# This is the source code of the library, I didn't make it up :)
class Dense(Layer):
# ... some initialisation here, like creating weights etc.
def call(self, inputs):
# Your Wx, the weights are also referred to as the kernel
# So self.kernel is your W
output = K.dot(inputs, self.kernel)
# Add the bias b if requested
if self.use_bias:
output = K.bias_add(output, self.bias, data_format='channels_last')
# Apply activation function if any
if self.activation is not None:
output = self.activation(output)
return output
Don’t worry if the code is unfamiliar but the concepts should be recognisable. The formulation of single layer can change depending on how the weights are represented / transposed. Books, courses and papers might use different notation, $W^Tx + b, Wx + b, xW + b$ etc. Now let’s make things more realistic by clarifying some terms you will see in deep learning libraries. This layer we presented here is often called a fully-connected or dense layer because every input is connected to every neuron. The number of outputs, i.e. the number of neurons you have in these layers is also referred to as units.
# From Keras library
keras.layers.Dense(units, activation='[the activation function]', ...)
# From Tensorflow, which is identical to Keras (literally it calls Keras)
tf.layers.Dense(units, activation='[the activation function]', ...)
# From PyTorch, opts to put activation as a separate layer
toch.nn.Linear(num_inputs, num_outputs, bias=True)
# From Chainer, yes there are many other libraries, although CHAINER IS DEPRECATED
chainer.links.Linear(num_inputs, num_outputs, nobias=False, ...)
### These all compute y = f(Wx+b) or y = Wx+b (if no activation)
All of the above examples compute what we defined as a layer. But you’ll notice there are some design differences which shouldn’t be a problem once you realise they are all trying to do same thing. Now in these libraries a layer is any encapsulation of computation, so you’ll have other layers such as convolutional keras.layers.Conv2D or even activation functions wrapped as layers keras.layers.Activation. It’s a nice way to encapsulate the building blocks of a network into manageable chunks from a software engineering point of view. The abstraction is that a layer computes some function on given inputs and it might contain some learnable weights.
Pro Tip: Maths is an ideal world of numbers whereas engineers need to deal with the reality. This situation manifests itself in design choices when implementing things. What these libraries have done is to follow the same maths (since mathematicians rule the world) but how they have done it slightly differ.
Feed-Forward Networks
Having the layer under our belt, we can now define what is referred to as a feed-forward, deep feed-forward or multi-layer perceptron (MLP) network. In the context of deep learning, these terms are used interchangeably. They are a collection of layers chained together.
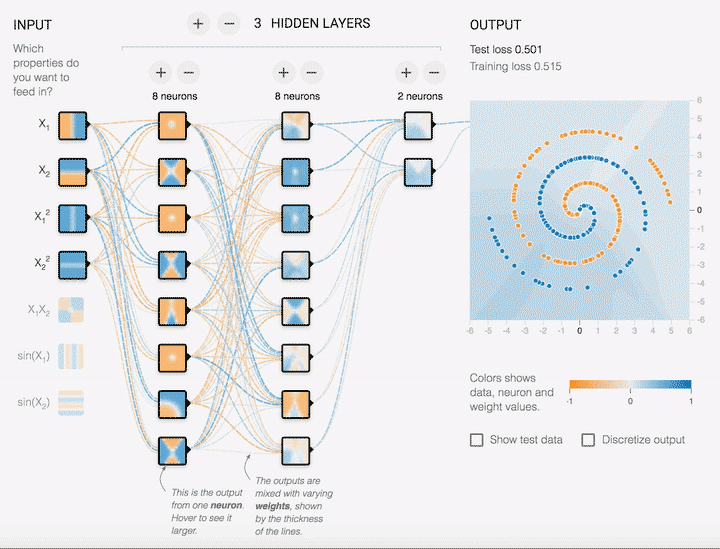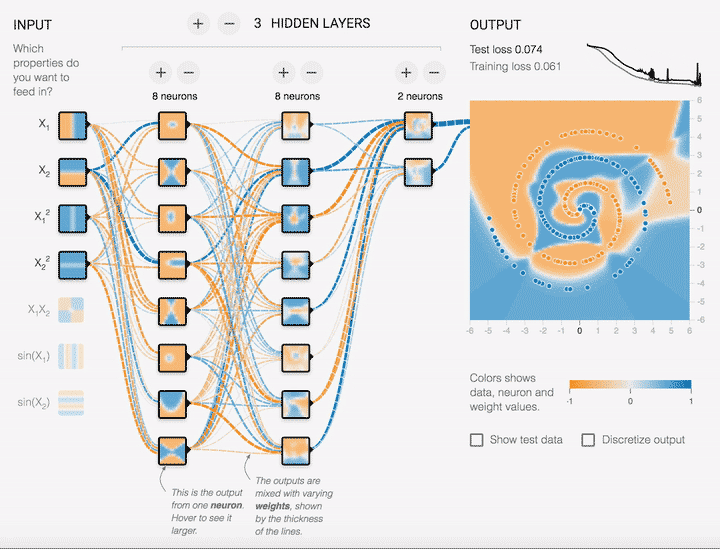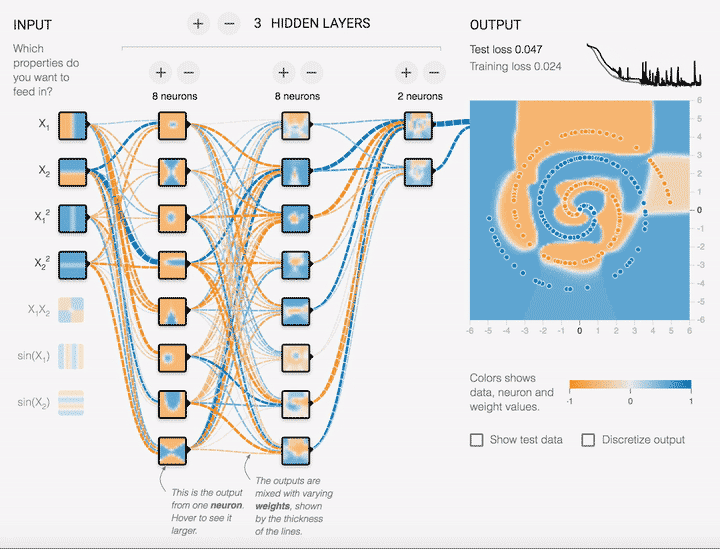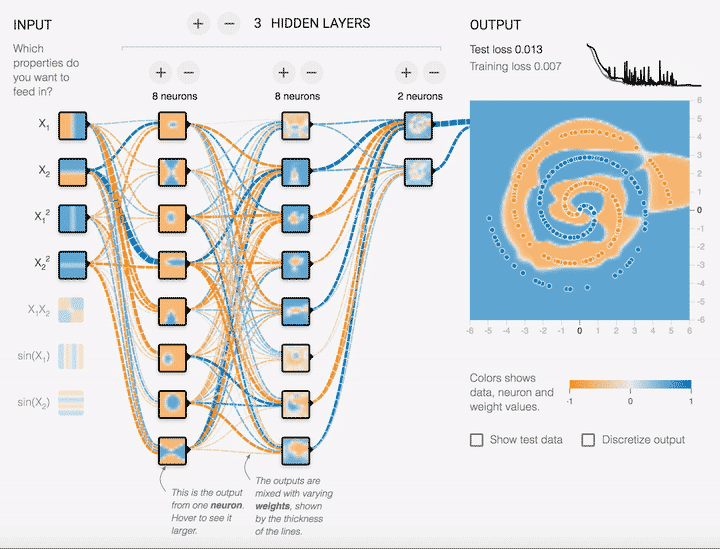
$$ y = h_3(h_2(h_1(x))) $$The construction of a feed-forward network is relatively straightforward, we just take some layers and connect the outputs of one to the inputs of the next one, here we noted a layer as $h_i$. The depth of the network is often referred to the number of layers while the width is the number of neurons. This is where the term deep learning comes from -> more layers more depth -> deeeeeeep learning. The architecture of a network refers to the overall structure: how many units the layers have, how these units are connected together (densely, recurrently etc). The layers in between the input and output are called hidden layers because they don’t interact with the outside world, they are hidden within the network. We also often do not explicitly place a layer for the inputs, since the input layer is conceptual rather than a layer that computes a transformation; it has no useful computation just $x = f(x)$. Here is a graphical view of a network with 3 layers (we exclude the input layer from counting):
Feed-forward Neural Network
In fact let’s implement this! Here is the Keras version of that exact diagram:
network = keras.models.Sequential() # one layer comes after the other
network.add(keras.layers.Dense(5, input_dim=4) # 4 inputs, 5 outputs
network.add(keras.layers.Dense(7)) # note we don't have to specify input size again, why?
network.add(keras.layers.Dense(3))
# that's it, we have a feed-forward network, let's also use it
network.predict([[41,42,42,43]]) # we get a vector of size 3
To be more rigorous let’s break down the mathematical steps of a network:
$$ y^{(l)} = f^{(l)}(z^{(l)}); z^{(l)} = W^{(l)} \cdot y^{(l-1)}; y^{(0)} = x$$The key thing to note is that the activation output $y^{(l)}$ becomes the input of the next one. The $z$ is often referred to as the pre-activation output of the layer. Note each layer has it’s own weights $W^{(l)}$. You’ll find different books represent this using different symbols depending on how sophisticated you want it to look but the idea is the same.
Initialising Weights
When we create a new network, what are the values of weights initially? Good question, glad you asked. We could rush ahead and set all the weights to 0 or 1, or to 42 which are all ways of initialising but there are more sound methods. Most deep learning libraries have weight initialising in built, for example Keras has numerous initialising functions. We will look at just a few and give the intuition behind the most common one. Let’s start with the basic ones:
- Zeros: just sets the corresponding parameters to 0. This is commonly used for the bias since initially you might not want any value for the threshold of a neuron. Zeros is the default initialisation function for the bias in the
keras.layers.Denselayer. - Normal: sets the parameters from a normal distribution $W \sim \mathcal{N}(\mu, \sigma^2)$ often setting the mean to 0 and variance to 1.
But just assigning random values might be troublesome. For example what if we get unlucky and assign small values, the outputs will start to vanish or assigning large weights will make things explode causing numerical overflows (remember we are running these on actual computers and the elegance of maths does not endure). So what we want is values to be random but vary in a reasonable range across the layers. In other words, we want the variance of the output of the layers to stay stable across the layers. Well why not just set it to fixed variance normal distribution for all layers and get it over with? Remember the layers are chained so when the computation is done that doesn’t correspond to a stable variance of the intermediate layers. To address this issue Xavier Glorot and Yoshua Bengio proposed a normalised initialisation method in their paper Understanding the difficulty of training deep feedforward neural networks; from section 4.2, “we suggest the following initialization procedure to approximately satisfy our objectives of maintaining activation variances and back-propagated gradients variance as one moves up or down the network”:
$$W \sim U[-\frac{\sqrt{6}}{\sqrt{n_j + n_{j+1}}}, \frac{\sqrt{6}}{\sqrt{n_j + n_{j+1}}}]$$where $U$ is the uniform distribution and $n_j$ is the number inputs of the layer and $n_{j+1}$ is the number of outputs. This initialisation is called Xavier or Glorot uniform, specifically glorot_uniform in the Keras library and xavier_uniform in PyTorch after the first author of the paper. The derivation of this method is beyond the scope but with many techniques it is important to understand the intuition behind the technique to be able to apply it. Just to re-iterate, their intuition is to keep the variance of the outputs of the layers equal to 1 so that the intermediate computations do not explode or vanish which in return creates a more stable training.
Pro Tip: Just because there are established ways of doing certain things doesn’t mean you shouldn’t experiment further.
Activation Functions
So far we just left $f$ on it’s own and didn’t really investigate the options available to us. So why on Earth do we have these activation functions? (Actually we would need these activation functions in space as well if we put a neural network on a space probe.) The only one we used was the threshold function which just set the output to 0 or 1. But we forgot to appreciate one crucial point: we want to learn beyond just linear functions. So $Wx + b$ on it’s own doesn’t allow us to learn non-linear functions such that the output varies non-linearly with respect to the inputs. Therefore, to introduce non-linearity into the network we apply non-linear activation functions.
Just to encourage the intuition more, we already saw a non-linear function XOR. If we just ignore the activation function or have $f(x) = x$, we cannot find a linear combination of the inputs that gives us XOR. Most of the problems neural networks tackle are non-linear: image classification, face recognition, speech recognition. There isn’t a linear combination of pixels that allows us to specify a cat per say.
Common activation functions
Let’s look at the most common activation functions, this is non-exhaustive, there are variants of these and other activation functions but these are the most commonly used ones:
- linear (identity) is the same as having no activation function. It is called linear because it exposes the linear transformation that often precedes the activation, $y = W^Tx + b$ directly. We are presenting it here for completeness.
- sigmoid compresses the output to the range between 0 and 1 with 0 corresponding to 0.5. It is also called the logistic function coming from logistic regression which views the activation function as a soft version of the threshold function we saw earlier. Instead of suddenly jumping from 0 to 1 at a given threshold, it varies smoothly.
- tanh adjusts the sigmoid such that input 0 now corresponds to output 0 and thus it ranges between -1 and 1. It is a scaled version of sigmoid.
- ReLU stands rectified linear unit. This activation is the most commonly used one for feed-forward networks since it preserves the desirable properties of a linear function while introducing non-linearity. It is a piece-wise linear function which means it is composed of linear functions but overall it is a non-linear function itself.
- softmax can be thought as the n-dimensional version of sigmoid, it compresses the sum of the output vector to be 1.
So what to use when? Well, in the hidden layers we often use ReLU to get the computational benefits and stability of the linear functions while having non-linearity. Can’t we just use the linear activation everywhere? No! That would just make things linear again:
$$ y = W^1 (W^2 x) = U x; U = W^1W^2 $$If we don’t use non-linear activations the entire network becomes linear as well! So ReLU is our closest friend. We can also use tanh or sigmoid in the hidden layers which works well for shallow classification networks but in general you’ll see by default it is a good idea to start with ReLU when using feed-forward networks and then experiment.
The output layer activation is special since it will work in tandem with the loss function. So the final layer activation will almost always depend on what we are trying to achieve with the network, is it binary classification, multi-class or just regression?
Loss Functions
The loss function is the function we are trying to minimise such that when we do so we learn the relationship between the given inputs and the desired outputs. It is crucial to select / design the correct loss function in order to be able to not only learn but also learn something meaningful. Therefore, the loss function depends on what we are trying to do and we’ll look at the most common cases we have.
Instead of just enumerating the loss functions there are, Keras loss functions, we will look at the common problems we face and the corresponding loss functions to use in those scenarios. We are taking a practical, problem first approach here.
Regression
When the task is to predict a continuous variable such as the velocity of a car, angle of a robot, house price etc we have a regression problem. What we will be doing is often called non-linear regression because the function we are trying to learn will be non-linear. It could be linear as well, no problem but if it is linear then a neural network is probably overkill. There are more sound, established ways to learn linear functions.
When we have such a problem we use the squared error loss function:
$$ L(y, \hat{y}) = (\hat{y} - y)^2$$which intuitively is 0 when the network output is same as the desired output. To make things clear, $\hat{y}$ is our network output and $y$ is the desired output. So when the training happens and we minimise the loss, we are gradually getting close the desired outputs. When there are multiple outputs, i.e. a vector as an output, we take the mean which yields the mean-squared error that is often used as the loss function in deep learning libraries. The $\hat{y}$ is our network output for the corresponding desired target, the final layer activation if you will.
$$ MSE(y, \hat{y}) = \frac{1}{d} \sum_j^d (\hat{y}_j - y_j)^2 $$# From Keras losses.py source code
def mean_squared_error(y_true, y_pred):
return K.mean(K.square(y_pred - y_true), axis=-1)
# Notice it uses vectorised functions rather than a for loop
What is the activation of the last layer? Since the output is not bounded, we often use linear activation when regressing with the squared error loss function. It allows to produce a continuous linear output which maps well to the target domain of house prices for example.
Classification
Perhaps the more common type of problems we encounter are classifying things which entails that our output is categorical (discrete). Given some input we want it to be labelled with one category, for example happy or sad. Binary classification refers to the situation when we have two classes and multi-class classification is when we have more than two. Mathematically, the binary case is just the multi-class with two classes, the equations are the same. In this context we are predicting one of many classes. That is really important, we assume every input belongs to one class and one class only. When we want to predict multiple classes / labels we have multi-label classification for example a molecule could be odourless and flammable at the same time.
Source: Tensorflow - Custom training: walkthrough
The figure above shows how we interpret the output of a neural network as probability distribution over possible classes. Doing so is not a coincidence because we utilise the principles of probability and information theory to choose an appropriate loss function.
| Type | Layer Activation | Desired Output | Loss |
|---|---|---|---|
| binary | sigmoid | 0 or 1 | binary cross entropy |
| multi-class | softmax | one-hot | categorical cross entropy |
| multi-label | sigmoid | 0s and 1s | binary cross entropy |
The above table summarises what we have for the classification family of problems. Let’s start with the activations. When we have a sigmoid output, the value ranges from 0 to 1. We can interpret this range as a probability of that input belonging to a class, i.e. the probability of the output given the input. As I said, we regard our network output to be a probability distribution over classes and we would like to maximise the likelihood of the network assigning the corrects labels to all inputs in our dataset:
$$ p(y|x; \theta) = \prod_i^N p(y^{(i)} | x^{(i)}; \theta) $$assuming that the examples are independent and identically distributed (i.i.d.) such that $p(A \cap B) = p(A)p(B)$. We get a product over all input output pairs. In the case of binary classification, we can regard the output of our network as the parameter of a Bernoulli distribution, the probability of success given an input. This yields the following expansion for the inner term:
$$ p(y|x; \theta) = \prod_i^N (\hat{y}^{(i)})^{y^{(i)}}(1- \hat{y}^{(i)})^{1-y^{(i)}}$$which is to say in the binary case the probability of one class is 1 minus the other; the $\hat{y}^{(i)}$ is our network output for the corresponding input. If we output the same label as the desired one for every pair we get 1, if we output the complete opposite then we get 0. So our job is to maximise this towards 1 in order to let the network predict the correct labels. We will take the logarithm because multiplying numbers strictly between 0 and 1 gives even smaller numbers such that the computer eventually gets a arithmetic underflow:
$$ \sum_i^N y^{(i)} \text{log}(\hat{y}^{(i)}) + (1-y^{(i)})\text{log}(1-\hat{y}^{(i)}) $$Note that maximising the logarithm is the same as maximising the original product, it preserves the objective and converts the previous equation into sums which are more robust and faster to compute by machines. Hence, this formulation allows us to work with a sum instead of product. Let’s take the inner equation defined on a single pair:
$$ L(y, \hat{y}) = -(y \text{log}(\hat{y}) + (1-y)\text{log}(1-\hat{y})) $$is the binary cross entropy loss function which is also referred to as negative log likelihood based on the equation. Notice the extra minus in front, this is because when optimising we often minimise the loss. So minimising the minus of the original equation maximises the quantity we are interested in. This can be extended to the multi-class situation:
$$ L(y, \hat{y}) = - \sum_k y_k \text{log}(\hat{y}_k) $$is the categorical cross entropy loss function where $k$ is the number of classes we have. In this situation we use softmax activation function in the final layer to get $\hat{y}$ which yields a probability distribution. For example, we can have $[0.2, 0.6, 0.2]$ with our desired output $[0, 1, 0]$ (one-hot encoded). Minimising this loss function will incrementally push our output towards $[0.0001, 0.9999, 0.0001]$ the desired output. To get an intuition as to why these are called cross entropy losses and possibly explore (not within the scope of this module) the information theory background of these loss functions have a look at the cross entropy formula:
$$ H(p,q) = - \sum_x p(x)\text{log}(q(x)) $$where $p$ and $q$ are probability distributions. Looking familiar? When we consider our network output and the desired outputs to be probability distributions, we end up with this cross entropy formula which stems from the KL divergence.
But in practice most libraries avoid computing exponents and taking logs naively and instead combine the operation into single loss function that takes the softmax and then log in a more numerically stable and efficient manner. For example, chainer.functions.softmax_cross_entropy asks for the pre-softmax activations, the output of final layer before applying the activation function and similarly torch.nn.cross_entropy. In these cases, the output layer activation is left as identity since the loss function applies it for us. However, in Keras we do specify the activation as softmax and the library handles internals since it provides a higher level API.
Pro Tip: Since we cannot represent numbers to an arbitrary precision, for example we have 32 bits for floating point numbers, we can get close to 1 such as 0.999987945 but perhaps not get exactly 1 because the updates get really really small. Most libraries compensate for numerical instabilities as numbers get really small, for example when we approach desired targets and the loss becomes infinitesimally small.
Can we not use just use squared error again with sigmoid activation? Yes, we can. Nothing will stop you from trying it out, in fact it will work to some extent. But, using a log based loss provides better convergence properties. Recall that the sigmoid has $e^{z}$ and the cross entropy loss has log, these cancel out and have a better defined slope / gradient allowing the network to converge better.
Training
It’s great, perhaps even entertaining to build these neural networks but they are useless with random weights. We need to train them on our data. As emphasised before, we need data. Data, data, data. BIG DATA? Once we have our data, we can consider how to train these neural networks.
Let’s try to specify what we mean by training. Our network has trainable parameters, weights (used interchangeably). So when we say we are training, we mean we are adjusting / modifying those parameters to fit the desired data. Cool. So all we need is a way to adjust the parameters such that the network gets better at predicting our data.
Pro Tip: When someone says they are training their neural network, it means they are wondering around aimlessly while the computer desperately tries to find the best parameters for their network. No one manually adjusts parameters by hand unless you are Jeff Dean who gets the best parameters at random initialisation.
Back Propagation
How do we know whether we should increase or decrease a weight? We need to understand how the weight affects our loss function. In other words, how does modifying one weight affect the loss function? If we know that, we can nudge the weight in the direction it minimises the loss function. For this, we use the derivative of the loss function with respect to the weight. We’ll assume you are familiar with taking derivatives and partial derivatives for this module. Intuitively, the derivative of a function with respect to a parameter $\frac{dy}{dx}$ tells us how $y$ changes when $x$ does. If you are unfamiliar with the concept, let’s consider this basic case:
$$ \begin{aligned} z &= x^2 + 4x - 3y + 10 \\ \frac{\partial z}{\partial x} &= 2x + 4 \\ \frac{\partial z}{\partial y} &= -3 \end{aligned} $$We are taking the derivative with respect to a variable at a time when we consider partials. Think of other variables to be just constants while taking a partial derivative with respect to a variable. So perfect, these derivatives are exactly what we need to understand the relationship between the loss function and the weights of the network. Then let’s take the partial derivative of the loss function with respect to the weights of a layer:
$$ \frac{\partial Loss}{\partial W^{(L)}} = \frac{\partial Loss}{\partial Y^{(L)}} \cdot \frac{\partial Y^{(L)}}{\partial Z^{(L)}} \cdot \frac{\partial Z^{(L)}}{\partial W^{(L)}}$$What just happened? We applied the chain rule of derivation to find the partial derivative of the loss function with respect to the weights since $Y=f(Z); Z=XW$. Notice we swapped XW to handle a collection of inputs at a time. This means $X \in \mathcal{R}^{N \times D}$ where is $N$ is the number of inputs and $D$ is the number of features of each input. This is also in vector form, we are taking the partial derivative of the loss with respect to every weight in the layer, because we want to adjust all of them. Let’s look at the hidden layer before the output layer:
$$ \frac{\partial Loss}{\partial W^{(L-1)}} = \frac{\partial Loss}{\partial Y^{(L)}} \cdot \frac{\partial Y^{(L)}}{\partial Z^{(L)}} \cdot \frac{\partial Z^{(L)}}{\partial Y^{(L-1)}} \cdot \frac{\partial Y^{(L-1)}}{\partial Z^{(L-1)}} \cdot \frac{\partial Z^{(L-1)}}{\partial W^{(L-1)}}$$It seems like a pattern is emerging here, as if we are almost following the forward computation backwards starting at the output and going backwards to the weights. Also notice that there is a repeated pattern which is reused for layers further down. This is the back-propagation algorithm, we propagate the gradients backwards through the network layers or in general back through the computation graph while storing repeated computations for efficiency. If we extract the pattern out it intuitively reads:
$$ \frac{\partial Loss}{\partial W^{(l)}} = \text{gradient w.r.t. my output} \times \text{gradient w.r.t. my weights}$$Why? When you wiggle (change the value of) $W^{(L-1)}$, it will affect $Z^{(L-1)}$ which will affect $Y^{(L-1)}$ which is the input to the next layer which affects $Z^{(L)}$ and so on. This occurs simply because that is how we wired things together, one layer connected to another.
Back-propagation of Gradients of a Linear Layer
The function could be anything, not just a dense layer. The algorithm holds for any computation graph: we compute some output, some error comes back and we compute the gradient with respect to our inputs and pass backwards whilst caching intermediate values to avoid redundant computation.
Now we will do the full derivation of a linear layer $Z = XW + B$ where $X \in \mathcal{R}^{N \times D}$, $W \in \mathcal{R}^{D \times M}$ and $B \in \mathcal{R}^{N \times M}$ such that $Z \in \mathcal{R}^{N \times M}$. The bias $B$ is the stacked version of $b \in \mathcal{R}^{1 \times M}$ to match the shapes. What is going on, why are we multiplying $XW$ and not the other way around. In practice, we never compute single data point at a time, we calculate everything in vector form. We put our engineering caps on and acknowledge that our inputs is a matrix of $N$ elements each with $D$ features. Imagine 10 people each with age, height and weight as input, we would get a matrix of $10 \times 3$ representing that input. So to compensate for that and keep things clear, we change the multiplication to be on the right $XW$ so the shapes match nicely. This is the convention used in most libraries, assume there is always more than one data point. Consider $N = D = 2; M=3$, let’s write things out clearly:
$$ \begin{bmatrix} x_{1,1} & x_{1,2} \\ x_{2,1} & x_{2,2} \end{bmatrix} $$$$ \begin{bmatrix} w_{1,1} & w_{1,2} & w_{1,3} \\ w_{2,1} & w_{2,2} & w_{2,3} \end{bmatrix} $$$$ \begin{bmatrix} \mathbf{b} \\ \mathbf{b} \end{bmatrix} = \begin{bmatrix} b_1 & b_2 & b_3 \\ b_1 & b_2 & b_3 \end{bmatrix} $$$$ \begin{bmatrix} x_{1,1}w_{1,1}+x_{1,2}w_{2,1}+b_1 & x_{1,1}w_{1,2}+x_{1,2}w_{2,2}+b_2 & x_{1,1}w_{1,3}+x_{1,2}w_{2,3}+b_3 \\ x_{2,1}w_{1,1}+x_{2,2}w_{2,1}+b_1 & x_{2,1}w_{1,2}+x_{2,2}w_{2,2}+b_2 & x_{2,1}w_{1,3}+x_{2,2}w_{2,3}+b_3 \end{bmatrix} $$This $Z$ will be used in the upper layers, we could apply an activation function then pass it as inputs to another layer. As far this layer is concerned, that is none its business, instead we only require that $\frac{\partial Loss}{\partial Z}$ is given to us. That gradient is passed by the upper layer which is using our outputs as their input. That is the gradient that comes our way, we have multiple outputs so that is also a matrix! Remember we are taking the derivative with respect every element here so we get a matrix of derivatives. Not to panic (yet):
$$ \frac{\partial Loss}{\partial Z} = \begin{bmatrix} \frac{\partial Loss}{\partial z_{1,1}} & \frac{\partial Loss}{\partial z_{1,2}} & \frac{\partial Loss}{\partial z_{1,3}} \\ \frac{\partial Loss}{\partial z_{2,1}} & \frac{\partial Loss}{\partial z_{2,2}} & \frac{\partial Loss}{\partial z_{2,3}} \end{bmatrix} $$tells us the gradient with respect to this layer’s outputs. We are interested in the gradients with respect to $W$, $b$ and $X$. We need $\frac{\partial L}{\partial W}$ and $\frac{\partial L}{\partial b}$ because we are going to be using them to learn, and we need $\frac{\partial L}{\partial X}$ to able to pass backwards (we can’t be selfish) to any other layers before us, if any. By the chain rule we know:
$$ \frac{\partial Loss}{\partial W} = \frac{\partial Loss}{\partial Z} \cdot \frac{\partial Z}{\partial W} $$$$ \frac{\partial Loss}{\partial b} = \frac{\partial Loss}{\partial Z} \cdot \frac{\partial Z}{\partial b} $$$$ \frac{\partial Loss}{\partial X} = \frac{\partial Loss}{\partial Z} \cdot \frac{\partial Z}{\partial X} $$Let’s even be more clear what these things look like:
$$ \frac{\partial Loss}{\partial X} = \begin{bmatrix} \frac{\partial Loss}{\partial x_{1,1}} & \frac{\partial Loss}{\partial x_{1,2}} \\ \frac{\partial Loss}{\partial x_{2,1}} & \frac{\partial Loss}{\partial x_{2,2}} \end{bmatrix} $$Since the loss is scalar value, notice how the derivative $\frac{\partial Loss}{\partial X}$ has the same shape as $X$, we have one value per input. This identical shape property holds for other partial derivatives too since they are all partials of the loss function which is a scalar. Let’s take just one element and investigate:
$$ \frac{\partial Z}{\partial x_{1,1}} = \begin{bmatrix} w_{1,1} & w_{1,2} & w_{1,3} \\ 0 & 0 & 0 \end{bmatrix} $$$$ \frac{\partial Z}{\partial x_{2,1}} = \begin{bmatrix} 0 & 0 & 0 \\ w_{1,1} & w_{1,2} & w_{1,3} \end{bmatrix} $$This can be obtained by looking at $Z$ finding where $x_{1,1}$ or $x_{2,1}$ occurs and taking the individual derivatives. Let’s plug it into the chain rule as well for just one element:
$$ \begin{bmatrix} \frac{\partial Loss}{\partial z_{1,1}} & \frac{\partial Loss}{\partial z_{1,2}} & \frac{\partial Loss}{\partial z_{1,3}} \\ \frac{\partial Loss}{\partial z_{2,1}} & \frac{\partial Loss}{\partial z_{2,2}} & \frac{\partial Loss}{\partial z_{2,3}} \end{bmatrix} \cdot \begin{bmatrix} w_{1,1} & w_{1,2} & w_{1,3} \\ 0 & 0 & 0 \end{bmatrix} $$Note the somewhat unconventional dot-product here, we are just multiplying every row with every other row and summing up. We do this to make things easier to understand. To be more strict we can flatten these matrices into vectors and perform the usual dot-product you are familiar with to obtain the same result. Another perspective is to consider this formulation with a single input $N=1$ then we would obtain a vector again. In this case, we obtain:
$$ \frac{\partial L}{\partial z_{1,1}}w_{1,1} + \frac{\partial L}{\partial z_{1,2}}w_{1,2} + \frac{\partial L}{\partial z_{1,3}}w_{1,3} $$Back-propagation of Gradients for a Single Element
Intuitively, how $x_{1,1}$ affects the loss is determined by the weights it multiplies with and then whatever is using that output upstream. Look at the paths from $x_{1,1}$ that lead to the loss function and the formulation should become more intuitive. Now we can repeat this for every element of $X$ and we get:
$$ \begin{bmatrix} \frac{\partial L}{\partial z_{1,1}}w_{1,1} + \frac{\partial L}{\partial z_{1,2}}w_{1,2} + \frac{\partial L}{\partial z_{1,3}}w_{1,3} & \frac{\partial L}{\partial z_{1,1}}w_{2,1} + \frac{\partial L}{\partial z_{1,2}}w_{2,2} + \frac{\partial L}{\partial z_{1,3}}w_{2,3} \\ \frac{\partial L}{\partial z_{2,1}}w_{1,1} + \frac{\partial L}{\partial z_{2,2}}w_{1,2} + \frac{\partial L}{\partial z_{2,3}}w_{1,3} & \frac{\partial L}{\partial z_{2,1}}w_{2,1} + \frac{\partial L}{\partial z_{2,2}}w_{2,2} + \frac{\partial L}{\partial z_{2,3}}w_{2,3} \end{bmatrix} $$Extracting out the gradients that were passed to us, we get:
$$ \begin{aligned} \frac{\partial Loss}{\partial X} &= \begin{bmatrix} \frac{\partial Loss}{\partial z_{1,1}} & \frac{\partial Loss}{\partial z_{1,2}} & \frac{\partial Loss}{\partial z_{1,3}} \\ \frac{\partial Loss}{\partial z_{2,1}} & \frac{\partial Loss}{\partial z_{2,2}} & \frac{\partial Loss}{\partial z_{2,3}} \end{bmatrix} \begin{bmatrix} w_{1,1} & w_{2,1} \\ w_{1,2} & w_{2,2} \\ w_{1,3} & w_{2,3} \end{bmatrix} \\ \frac{\partial Loss}{\partial X} &= \frac{\partial Loss}{\partial Z} W^T \end{aligned} $$Phew, that wasn’t all that bad. In books you’ll see people replacing intermediate results with different symbols such as $\delta$ to encapsulate some steps, we just went all guns blazing and wrote the thing out instead of making a soup Greek letters. Remember, the derivation follows the journey of a single element and then we generalised into the matrix form. In a similar fashion, we can look at a single weight:
$$ \frac{\partial L}{\partial z_{1,1}}x_{1,1} + \frac{\partial L}{\partial z_{2,1}}x_{2,1} $$which captures how $w_{1,1}$ affects the output and when we perform the same analysis on every weight, we get this beauty:
$$ \begin{bmatrix} \frac{\partial L}{\partial z_{1,1}}x_{1,1} + \frac{\partial L}{\partial z_{2,1}}x_{2,1} & \frac{\partial L}{\partial z_{1,2}}x_{1,1} + \frac{\partial L}{\partial z_{2,2}}x_{2,1} & \frac{\partial L}{\partial z_{1,3}}x_{1,1} + \frac{\partial L}{\partial z_{2,3}}x_{2,1}\\ \frac{\partial L}{\partial z_{1,1}}x_{1,2} + \frac{\partial L}{\partial z_{2,1}}x_{2,2} & \frac{\partial L}{\partial z_{1,2}}x_{1,2} + \frac{\partial L}{\partial z_{2,2}}x_{2,2} & \frac{\partial L}{\partial z_{1,3}}x_{1,2} + \frac{\partial L}{\partial z_{2,3}}x_{2,2} \end{bmatrix} $$We again extract out the gradients that were given to us:
$$ \begin{aligned} \frac{\partial Loss}{\partial W} &= \begin{bmatrix} x_{1,1} & x_{2,1} \\ x_{1,2} & x_{2,2} \end{bmatrix} \begin{bmatrix} \frac{\partial Loss}{\partial z_{1,1}} & \frac{\partial Loss}{\partial z_{1,2}} & \frac{\partial Loss}{\partial z_{1,3}} \\ \frac{\partial Loss}{\partial z_{2,1}} & \frac{\partial Loss}{\partial z_{2,2}} & \frac{\partial Loss}{\partial z_{2,3}} \end{bmatrix} \\ \frac{\partial Loss}{\partial W} &= X^T\frac{\partial Loss}{\partial Z} \end{aligned} $$Similarly when we look at the bias we obtain:
$$\frac{\partial Loss}{\partial b} = \mathbf{1}^T\frac{\partial Loss}{\partial Z}$$but the individual steps of doing so is left for you as an exercise. Above, $\mathbf{1}$ is a column vector of ones. Until the birth of accessible deep learning libraries, people computed these gradients themselves. But once the derivation is done, all the deep learning libraries nowadays compute the gradients automatically using these derivatives. For example, the AutoGrad package of PyTorch is dedicated for this. Let’s look at an example using Chainer:
# For a more concrete example consider
# this snippet using the Chainer library
import chainer
x_data = np.array([5], dtype=np.float32)
x = chainer.Variable(x_data)
# this is the forward computation
y = x**2 - 2*x + 1
print(y) # variable([16.])
# compute and backpropagate gradients
y.backward()
# gradients propagated to x
x.grad == [8.]
# --- what is y.grad ? ---
Pro Tip: Beyond as a learning exercise, if you ever find yourself computing gradients manually for basic operations either you are on verge of inventing something or you are not using a deep learning library to do it for you.
What about an activation function? Suppose we again have $Z = f(X)$ where $X \in \mathcal{R}^{N \times D}$ and $Z \in \mathcal{R}^{N \times D}$. Note we are applying the function to every element:
$$ \begin{bmatrix} f(x_{1,1}) & f(x_{1,2}) \\ f(x_{2,1}) & f(x_{2,2}) \end{bmatrix} $$This time we only need the derivative with respect to $X$, and using the chain rule we know:
$$ \frac{\partial Loss}{\partial X} = \frac{\partial Loss}{\partial Z} \cdot \frac{\partial Z}{\partial X} $$Applying the same one element at a time analysis, we look at $x_{1,1}$:
$$ \begin{aligned} \frac{\partial Loss}{\partial x_{1,1}} &= \begin{bmatrix} \frac{\partial Loss}{\partial z_{1,1}} & \frac{\partial Loss}{\partial z_{1,2}} \\ \frac{\partial Loss}{\partial z_{2,1}} & \frac{\partial Loss}{\partial z_{2,2}} \end{bmatrix} \cdot \begin{bmatrix} f'(x_{1,1}) & 0 \\ 0 & 0 \end{bmatrix} \\ &= \frac{\partial Loss}{\partial z_{1,1}} f'(x_{1,1}) \end{aligned} $$where $f'$ is the derivative of our activation function. From an intuitive point of view, our input only affects one output and that depends on how much the activation function affects the output. Generalising to matrix form again:
$$ \begin{aligned} \frac{\partial Loss}{\partial X} &= \begin{bmatrix} \frac{\partial Loss}{\partial z_{1,1}} f'(x_{1,1}) & \frac{\partial Loss}{\partial z_{1,2}} f'(x_{1,2}) \\ \frac{\partial Loss}{\partial z_{2,1}} f'(x_{2,1}) & \frac{\partial Loss}{\partial z_{2,2}} f'(x_{2,2}) \end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial Loss}{\partial z_{1,1}} & \frac{\partial Loss}{\partial z_{1,2}} \\ \frac{\partial Loss}{\partial z_{2,1}} & \frac{\partial Loss}{\partial z_{2,2}} \end{bmatrix} \circ \begin{bmatrix} f'(x_{1,1}) & f'(x_{1,2}) \\ f'(x_{2,1}) & f'(x_{2,2}) \end{bmatrix} \\ &= \frac{\partial Loss}{\partial Z} \circ f'(X) \end{aligned} $$where $\circ$ is element-wise multiplication (also known as Hadamard product). Just like the linear layer, this holds for every activation function. One equation to rule them all.
Derivatives of Common Activation Functions
Here are derivatives of some activation functions:
- linear: $f'(x) = 1$ for any given $x$.
- sigmoid (logistic): $f'(x) = f(x)(1-f(x))$ really neat no? The derivative can be defined using it self.
- tanh: $f'(x) = 1 - f^2(x)$ again we can define the derivative using the function itself here.
- ReLU: $f'(x) = 1$ if $x > 0$ otherwise it is just 0 as well. Looking at the function gives it away.
This is also an appropriate time to discuss why ReLU is preferred. If you look at the gradients of sigmoid and tanh they strictly range between 0 and 1. So when you have a very deep network, you multiply these as you back-propagate which causes the gradients to vanish. This is the vanishing gradient problem and it makes training deep neural networks very difficult. If you had 50 layers, the first layer will get tiny tiny gradients to update its weights with, almost not training at all. When we use ReLU; however, this problem is somewhat mitigated as it’s derivative is a constant 1 not causing any vanishing on its own.
Gradient Descent
Now we have the direction we need to nudge the weights of our network in order to minimise the loss. What do we do? We just iteratively descend in the direction of the gradient slowly minimising the loss which is referred to as gradient descent. Gradient descent is a general optimisation technique and is not in any way special to neural networks. You can optimise linear models using their gradients as well for example, or anything you can compute the gradient of.
Example error surface with respect to two parameters
We start with random weights / parameters $\theta$ then we compute the gradients with respect to some data and loss function, also called an objective function denoted $J(\theta)$, adjust weights in that direction and repeat until we reach some minimum. As the image shows, a non-linear function can have multiple local minimum with respect to the objective function. We can descend in two different directions, which direction is better? We don’t know at this point so we take a leap in one direction and might end up in an undesirable minimum. Although we can only visualise this error surface with respect to two parameters, the principle is similar in higher dimensions. There is no guarantee we will converge to the global minimum when just walk in the direction of the gradient.
Pro Tip: You see a village in the distance and start walking in that direction. Although you will get closer to the village that doesn’t mean you will arrive at it, you could get stuck at some hill or cliff.
So what do we actually do? We update the weights using the gradient:
$$ W \leftarrow W - \alpha\frac{\partial L}{\partial W}$$where $\alpha$ is the learning rate that tells us how much of a leap we should take in that direction. At each update, we slowly adjust the weights in the direction that minimises the loss that is given by the gradient we computed. We often set $\alpha = 0.01$ or $0.001$, essentially something small but it depends on the problem.
Source: Medium - Machine Learning 101
An important observation is that we assumed that the gradient could be computed for every parameter. This is very important, we need our functions, network and loss to be differentiable in order to use this method. What if they are not? There are other algorithms such as genetic algorithms that do not use the gradient to optimise the network parameters.
Pro Tip: Like many things in life, there are many ways of doing the same thing. Gradient descent and neural networks represent just few pages of a big book called artificial intelligence.
Ideally we would like to compute the gradient using the entire training data, but that is computationally expensive and slow if for example we have thousands of data points. Instead we estimate the true gradient using small random batches:
- Stochastic Gradient Descent (SGD): in it’s vanilla form takes one random data point and immediately updates the weights using that gradient.
- Batch Gradient Descent: uses the entire data set and then updates the weights.
- Mini-batch Gradient Descent: takes small batches such as 32 data points at a time and then updates the weights.
But in practice we just refer to mini-batch as batch and mini-batch gradient descent as stochastic gradient descent. This is the ugly truth:
# Keras library
network.compile('sgd', 'mse') # mse is mean squared error here
network.fit(X, Y, batch_size=32, epochs=40, shuffle=True)
where batch_size is actually the mini-batch size, the first dimension of the input $X \in \mathcal{R}^{N \times D}$. Let’s break down what is going on here:
- We take training data of size $N$ each with $D$ features, a matrix $N \times D$ if you will.
- We shuffle it so the network doesn’t see the same data points grouped together, this helps with convergence since different combinations of data points can give different useful gradient estimations.
- We chop it into batches of size $B$, so we get a batch of shape $B \times D$. How many batches are there? $N/B$ many.
- We compute the forward pass to collect the network output one batch at a time.
- We compute the derivative of the loss with respect to the network outputs.
- We then back-propagate the gradients to compute the derivative of the loss with respect to every parameter in the network.
- We update the weights using the given learning rate.
- We repeat 4 to 7 for every batch.
- Once we do this for every batch, we finished an epoch, a full run over our training data. Now we repeat from 2 to 8 until we have done the required number of epochs or reached a convergence criteria.
Now we will not explicitly make a soup of Greek letters to formally define that process. Instead let’s focus on something more important. Notice we are only updating the weights of the network, what about all the other stuff that forms a network such as number of layers, number of units in each layer, the learning rate? Anything that is not learned and is set by the user is a hyper-parameter. It is up to the user to find, guess or tune until this entire training process gives desirable outputs. In fact, most researchers try different sizes, number of layers and report the best one they get. You can methodically search for it as well for example using grid search although it can be very expensive to do so. Training large networks currently takes days, we often cannot afford to try a hyper-parameter tuning sweep.
Different learning rates on gradient descent
Although currently the learning rate is fixed, there are many extensions to gradient descent that make it adaptive such that the training becomes more efficient. The simplest of them is learning rate decay which reduces the learning rate by a factor each epoch:
$$ \alpha \leftarrow \alpha d $$where $d \in [0, 1]$. The idea is we reduce the rate as we approach the minimal loss, so take smaller steps to not overshoot. More sophisticated methods such as having a one learning rate per parameter also exist and they span their own family of gradient descent algorithms such as RMSProp, AdaDelta and Adam which are not within the scope of this module.
Source: CS231 Stanford - Credit: Alec Radford
Evaluating
So you are training your neural networks and everything is fine, the loss is going down, the model seems to be learning something. Is it? To ensure that our networks, models are learning something beyond just the training data which is what we use to train with, we need test or validation data that are separate from training. The model, network never ever trains on the test or validation data points! You’d be surprised how easy it is make a mistake in the code sometimes. What is the difference between validation and test data? We use the validation data to tune the hyper parameters of the model, changing number of layers, units etc. Then the best model on the validation set becomes our final model to test on the test data we have. We can’t tune hyper parameters on the test data because then the test data becomes part of the training again!
Source: Wikimedia Commons
Where on Earth do we get validation or test data? We partition the overall data set. For example if we have 10000 data points, we could do a 0.1, 0.1 test validation split to get 1000 test points, 1000 validation points and 8000 training points. Keras has the validation split option built-in, model.fit(X, Y, validation_split=0.1, ...) for example will split the overall data $X$ and $Y$ into two partitions of ratios 0.1 and 0.9 for validation and train respectively. Some data sets come with pre-set train, validation and test splits. We also often use k-fold cross validation which just means we take $k$ many different random train-validation-test splits / folds (preferably non-overlapping) to reduce bias.
The more important question is why do we need this separation. Neural networks can learn very complex non-linear functions, which means they are in danger of learning patterns specific to or even memorising the training data. Imagine we have 100 data points and a neural network with 100 units in the hidden layer. Every unit can learn which input it is and we can predict based on that, no actual learning that we are interested in is done.
Over-fitting
Under and over fitting in a simple dataset
Looking at the training data in the image, we ideally want a smooth boundary since the single yellow point around the blue territory seems like noise which are data points that do not fit with the rest of data, they are somewhat like outliers, having an actual dog image and saying it’s a cat. When the network learns a very specific boundary, we say it starts to over-fit. In order words, over-fitting occurs when the network learns properties specific to the training data rather than the general paradigm. Similarly, under-fitting happens when the network cannot learn the training data at all.
Point of overfitting and early stopping
How do you know this is happening? Looking at the loss value or accuracy over time with respect to training and validation data gives it away. Initially both training and validation loss start decreasing as the network learns something about the data, but at some point the validation loss starts to increase while the training loss continues to decrease. That is often when over-fitting starts to happen. The network is learning things that do not apply to the validation set, things that are specific to the training set since the loss for the training continues to decrease. The analysis for the accuracy would be the inverse of the loss as in the accuracy of validation would start to decrease or stop improving when the training accuracy continues to increase.
One method for avoiding over-fitting is to simply stop early. Very cleverly, this is called early stopping. It stops the training as the validation loss starts to stray away from the training loss, we stop. Keras implements this in keras.callbacks.EarlyStopping and it is a very simple but very useful tool.
Pro Tip: If you come up with a very useful algorithm that is very simple like early stopping, you are allowed to name it early stopping. For example, a door stopper is a very very useful thing and it is aptly named a door stopper.
There is a correlation between the network capacity and over-fitting. The capacity refers to the number of layers and units those layers have. More layers, more units means the network has more parameters and therefore a bigger capacity to learn more complex functions. Here is some advice on what to do:
- if the network is not learning on the training data, i.e. the loss is not decreasing at all and it’s under-fitting, then it might not have enough capacity to learn. We can try increasing the number of units and/or the number of hidden layers. Don’t go crazy with the numbers, make them as small as possible but not smaller.
- If the network is over-fitting, that is the validation is increasing while the training loss is decreasing, it has too much capacity and we can look at either reducing it by lowering the number units, layers or apply regularisation.
Best solution to any over-fitting problem is to GET MORE DATA. If we have more data, we won’t need to reduce capacity since there will less and less opportunity for the network to memorise or learn specific things about the training set as we have more training points. But this is rarely the case in practice… We don’t have infinite number of cat images (thank goodness).
Regularisation
Often we want larger networks to learn more complex patterns in our input data but that means we have too much capacity and a tendency to over-fit. Regularisation is way to penalise the model in some way to stop it from over-fitting. Another way of looking at it is we are reducing the effective capacity of the network for example by penalising how large the weights could be.
Source: Wikimedia Commons
One way the model can over-fit is if it’s weights are allowed to grow out of control. Why? If there is a very useful feature that describes only the training data, the network will latch onto the information to learn the function, but the validation data might not have that. So we end up with the blue line in the image, it aggressively finds a way to learn the training data. But we can penalise this using:
$$ \begin{aligned} J(\theta) &= Loss(y, \hat{y}) + \lambda \sum_w w^2 \\ w &\leftarrow w - \alpha (\frac{\partial Loss}{\partial w} + 2\lambda w) \end{aligned} $$The L2 regularisation adds the squared weight $w^2$ to the objective function along side the loss. So if the weight gets larger, so does the loss, in effect to reduce the loss the network needs to keep the weights small as well. The $\lambda$ tells how much we want to regularise, we usually set it to 0.01. The effect is seen on the weight update rule, now the update is proportional to the weight itself; thus large weights shrink proportionally faster.
$$ \begin{aligned} J(\theta) &= Loss(y, \hat{y}) + \lambda \sum_w |w| \\ w &\leftarrow w - \alpha (\frac{\partial Loss}{\partial w} + \lambda \text{sign}(w)) \end{aligned} $$The L1 regularisation just adds the absolute value of the weight itself to the objective function. The update rule now considers a fixed movement towards 0. If the weight is negative it is always nudged upwards, if it is positive it is always nudged downwards by a fixed $\lambda$ amount towards 0. Both L1 and L2 are sometimes are referred to as weight decay which stems from the fact that they both decay the weights towards 0.
# From Keras library source code, I didn't write this, it is the library itself
class L1L2(Regularizer):
"""Regularizer for L1 and L2 regularization.
# Arguments
l1: Float; L1 regularization factor.
l2: Float; L2 regularization factor.
"""
def __init__(self, l1=0., l2=0.):
self.l1 = K.cast_to_floatx(l1)
self.l2 = K.cast_to_floatx(l2)
def __call__(self, x):
regularization = 0.
if self.l1:
regularization += K.sum(self.l1 * K.abs(x))
if self.l2:
regularization += K.sum(self.l2 * K.square(x))
return regularization
# This gets added to the overall objective function
So why does this help with over-fitting? Recognise that both methods push weights towards 0, a weight of 0 means no connection. No connection means less capacity so in effect we are simplifying the network which removes its ability to learn very specific patterns of the training set.
One common feature mentioned for the L1 regulariser is that it produces sparse weights. Intuitively it pushes most of the weights to 0, so only the most useful features will need to have non-zero weights for the network to learn / predict the patterns in the data. This sparsity leads to what is called feature selection, the training causes the layer on which L1 regularisation is applied to select few inputs to produce an output in order to keep the weights small. L2 on the other hand ensures smoothness, so it encourages a combination of inputs / features to be used since weights are not forced towards 0 when they are already small. A layer with L2 thus tries not to rely on any few features but a large combination of them. We can mix these, so in the final layer we might want to pick certain features and use L1, in the hidden layers we might use L2.
Dropout
So if pushing the weights towards 0 essentially cuts the connection and reduces the capacity of the network, why don’t we just remove them entirely and not have fully-connected layers? Well, that is exactly what dropout does: it randomly sets outputs of layers to 0 essentially turning off neurons. It is very simple, don’t believe me? Here is the title of the paper that published the idea -> Dropout: A Simple Way to Prevent Neural Networks from Overfitting:
Source: Dropout: A Simple Way to Prevent Neural Networks from Overfitting
With probability $p$ we set the output of the neuron to 0. The name stems from the fact that we drop certain neurons by setting their output to 0. There isn’t much to it, but what is fascinating is why it works to help reduce over-fitting. Looking at the diagram, every time we apply dropout we get a different sub-network. It is as if we are training smaller networks inside a larger one which reduces inter-dependency between neurons across layers since it might be dropped next round. So the overall network learns to be more robust with less ability to extract specific features of the training data. Dropout is only applied at training time. At test or prediction time the entire network is active and no neuron is dropped but the weights or the activations might be scaled in order not to saturate neurons with all connections active.
Source: Medium - Regularization in deep learning
Since we basically dissect our network into smaller ones during training, we might need more epochs to train it increasing the overall training time. This is often worth for getting better generalisation, i.e. not over-fitting. Another important aspect to consider is the gradients become 0 as well so a higher learning rate or an adaptive learning rate algorithm such as Adam would be helpful. Gradients from certain paths in the network are cancelled so the gradients are smaller, so we need to adjust the learning rate to adapt for that or again increase training time.
Data Pre-Processing
Although getting more data is always the best option, more often than not we can better utilise our data by applying some pre-processing. Our objective is still to stabilise training and not over-fit. Ultimately what our network is trying to learn depends on the data, so if there are trivial relationships in the training data it might over-fit. For example, imagine in our training data every person who is taller than 80cm is over 25 years old but in our validation data we have people who are also below 25. If we are learning a relationship between height and age, the training data suggests you need to be above 25 for 80cm, easy. But that is not true for the general population, our validation or test sets.
One common approach is to do data augmentation which enhances our existing data. For example if we have some numerical data we can introduce some noise to it:
$$ X' = X + \mathcal{N}(\mu, \sigma^2)$$Why does adding noise help? Because if there are any specific features / points the network learns, we now wiggle them around using some Gaussian noise so they are not static anymore. To look at it another way, we are generating artificial data based on the original data; more data (though noisy) gives better generalisation and reduces over-fitting. Other common ways of data augmentation include:
Basic data augmentation through rotation, translation and blur on the MNIST digit 6
- Blurring, flipping images: a cat is still cat if it is slightly blurred or flipped horizontally.
- Replacing words with synonyms in sentences. Replacing happy with joyous still keeps the sentence positive for a sentiment classification. It might change how positive so we need to be careful what is acceptable data augmentation.
Perhaps a more common technique is data normalisation in which the input and potentially the output data is normalised. For example we can map the largest value to $b$ and smallest value to $a$:
$$ X' = a + \frac{(X-X_{min})(b-a)}{X_{max} - X_{min}} $$is called feature scaling because we apply a fix scaling on the data. We often reduce the range to $[0,1]$ or $[-1,1]$. Similarly we can normalise using the mean and standard deviation of the data:
$$ X' = \frac{X-\mu}{\sigma} $$which makes the data have mean 0 and standard deviation 1. This normalisation is often applied when we know the input is normally distributed, such as height of people. It is also referred to as z-normalisation, standard score or z-score normalisation since we are mapping our data to the unit normal distribution $\mathcal{N}(0, 1)$.
Why does normalisation help? To get a better intuition let’s re-visit the derivative of the linear layer:
$$\frac{\partial Loss}{\partial W} = X^T\frac{\partial Loss}{\partial Z}$$Notice how the $X$, our actual input appears in the equation if this was the first hidden layer in network. So updating weights which uses this gradient relies on the magnitude of the input. Thus, having really large or really small inputs destabilises or hampers training respectively. When we normalise our data to reasonable ranges or distributions, we ease this problem. Similarly, with ReLU activation things can get really large since it’s unbounded, thus having normalised inputs helps.
Pro Tip: Piling up a column of bricks doesn’t make a house, instead one must understand how the bricks build together. Similarly, applying all these regularisation techniques might not solve or even worsen the situation if you don’t think about what effects these have.
Full Example
Now we have everything we need to learn something. Just like printing "Hello World!", with neural networks things start on recognising hand-written digits. This is the benchmark MNIST dataset:
Source: Wikimedia Commons
Our objective is to learn what digit a given hand-written image corresponds to. Is this binary, multi-class or multi-label classification? Let’s dive into it with the example code from the Keras library, the code is exactly the same but I will add some comments to relate back to what we covered so far:
'''Trains a simple deep NN on the MNIST dataset.
Gets to 98.40% test accuracy after 20 epochs
(there is *a lot* of margin for parameter tuning).
2 seconds per epoch on a K520 GPU.
'''
# From https://github.com/keras-team/keras/blob/master/examples/mnist_mlp.py
from __future__ import print_function
# the above line makes print functions compatible with Python 2
# so the code runs on both Python 2 and 3, you should use Python 3
import keras
# Keras has some benchmark datasets ready built-in such as MNIST
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.optimizers import RMSprop
# We set the batch size and epoch hyper-parameters here
batch_size = 128
num_classes = 10
epochs = 20
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784)
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
# Can you recognise what this is doing to the data?
x_train /= 255
x_test /= 255
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# It is always a good idea to print as you go along
# to get feel of the data, processing etc you are doing
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
# this is your one-hot encoding, it takes indices of targets
# and converts them to vectors of size num_classes each
# where they have a 1 at the specified index
# this target is the digits, 0,1,2,3,4,5,6,7,8,9
# This is the network or model, our feed-forward network
# or multi-layer perceptron, can you tell how many layers it has?
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dropout(0.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(num_classes, activation='softmax'))
# notice how dropout is added after each hidden layer
# not a trick question but why isn't there dropout after the final layer?
model.summary() # this prints a nice summary of the model
# it also tells how many weights / parameters your model has
# We now select our loss function, the optimiser, and any extra metrics we want
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
# They use RMSProp and I left it as is in case you want to explore beyond the course
# but recognise it is just an extension of our vanilla gradient descent.
# This is the training loop, where we update the weights of the network
history = model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))
# Finally we get the loss and accuracy on our test set to see how well
# our model generalised or over-fitted etc.
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
If there is anything unclear in the above code conceptually then I recommend going through those bits from the notes again to understand what is going on behind the scenes in a high-level deep learning library. The programming quirks, the design of the library, how the layers are used etc are not necessarily important as they vary from library to library. I chose Keras here since it is easy to follow and the abstractions map well to the concepts we covered.
Concluding Remarks
Like with other machine learning methods, neural networks are a tool and should be treated as such. They are not the solution to everything although they can solve very interesting problems. These lecture notes cover most of the fundamental concepts that would allow you to continue exploring. I’m sure there are things some would argue should be included in these notes and some topics to be removed. I concur and invite them to fork the repository.
Rest assured, some of the suggestions made in these notes might not be suggestible in few years time. The field surrounding neural networks is moving forward at an alarming rate, most people are unsure what they are learning, how can multiplying floating point numbers recognise what I’m saying while some believe it will allow the machines to take over the world. Only time will tell what is to come unless we machine learn the future in the present using the past and start predicting what is to come. If you just got excited about that, I recommend reading these notes from the very beginning.
Pro Tip: Just because someone says this is all the material you need to know for the exam doesn’t mean this is all there is to know. You should explore beyond the boundaries of any given knowledge.